其他
游戏
影视
观后感
心理
聊天记录
数位dp
[toc]
概念和场景#
做法#
模板#

1 | private int f(int i, boolean isLimit, boolean isNum) { |
相关题目#
902. 最大为 N 的数字组合 - 力扣(LeetCode)
https://leetcode.cn/problems/number-of-digit-one/
2022年10月
[toc]
2022-10-20#
2269. 找到一个数字的 K 美丽值 - 力扣(LeetCode)
字符串截取一段的函数是substring(起始位置闭区间, 终止位置开区间)
注意0不能用来取余
2022-10-13#
取前后石子的博弈论#
先是用dp动态规划+博弈论求解
1 | class Solution { |
然而实际上先手方可以做到一直只取奇数位, 或者只取偶数位,那么只要求出奇数位总和和偶数位总和拿个大即可,所以先手必胜。
分块排序最终有序问题#
我先是用了一个O(n^2logn)的麻烦方法, 欺负他量级小。
1 | class Solution { |
实际上应该是 如果 当前最大值且正在在对应位置, 则左边的都可以排序了,因为自己一定是稳定排的(左边没有比自己小的,而自己又正好在自己这个值的索引处,那么左边肯定能排)
1 | class Solution { |
2022-10-12#
负二进制问题#
模拟了半天才知道规律好头疼。下面这个感觉很难记住,其实就是
-1的时候,此位变1,下一位+1
1的时候,此位变1,下一位-1
0的时候不变


提交二里看到一个,没看懂怎么利用

1 | class Solution { |
presto性能优秀原理和性能优化
[toc]
性能优秀的几个要点#
1. 完全基于内存的并行计算#
不考虑存盘,因此很多操作都尽可能设计成在内存完成,几乎不考虑落盘的可能性。
2. 流水线计算#
只要Task中的算子从上游Task中可以获取到数据,便开始执行计算,计算产出的数据直接放入该Task对应的OutputBuffer中等待下游Task来访问,也就是说在执行非聚合算子的情况下,Client是可以源源不断的流式获取到计算结果,而不用等到所有数据都计算完成
3. 本地化计算#
Presto会根据元信息读取分区数据,提供的conectorApi可以适配不同的数据源做本地数据读取
合理的分区能减少Presto数据读取量,提升查询性能。
且可以提前本地计算,包括支持broadcast-join
4. 动态编译执行计划#
原始的逻辑执行计划,直接表示用户所期望的操作,未必是性能最优的,
逻辑执行计划fragment发送到机器上后,由结点树形式转写成operator list,根据逻辑代码动态编译生成字节码。动态生成字节码,主要是利用编译原理:
-
展开循环
-
根据数据列的类型,直接调用对用的函数,以减少分支跳转语句。
这些手段会更好的利用CPU的流水线。
5. 小心使用内存和数据结构#
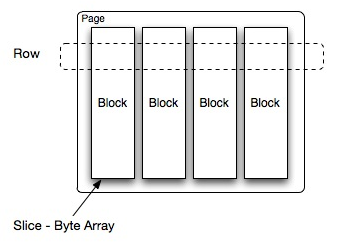
对于数据的计算是以Page为单位,
Page是由多个Block组成,每个Block为单一类型
例如Int Block, Long Block, Varchar Block等,其代表了Table中的某一列中的部分数据
因此数据可以被成为列数据
6. 类BlinkDB的近似查询#
支持提供一个近似查询函数
例如approx_distinct() 函数比Count(distinct x)有大概2.3%的误差
近似查询概念:
如果数据库所存放的数据的数量十分庞大,要完成完整查询,则会需要花费较长的时间。如果我们使用近似查询技术,就可以以采样的方式,对均值的结果进行估计,以一定的精度损失,快速的获取对精确值的估计。这在某些场景下,会有一定的应用。不止是COUNT,SUM,AVG等常用的聚集估计方法都可以得到支持。除了简单的查询之外,近似查询还可以处理关联查询(join),嵌套查询,范围查询等复杂查询场景。
7. GC控制#
https://www.zhihu.com/question/461560750
https://www.sohu.com/a/310831715_115128
https://zhuanlan.zhihu.com/p/93711386
presto性能调优的几个方式#
Presto性能调优的五大技巧
Presto介绍与常用查询优化方法
提升并行度#
通过task.concurrency参数来设置join、aggregator等操作的并发度
但这个并行度是分多线程,还是用于控制多诘?
提升worker处理spilt的线程数#
如果工作器CPU利用率低并且所有线程都在使用中,则增加task.max-worker-threads
可以提高吞吐量,但是会导致堆空间使用率增加。将该值设置得太高可能会由于上下文切换而导致性能下降。(看起来并行度指的是节点并行度?)
worker中由于采用线程模型,因此Query对应算子的执行会从线程池中分配一个线程负责,而该线程对于Operator的执行时长为duration表示,超过duration所表示的时间,该线程就有机会切换执行其他query的算子,从而从粗粒度实现用户态CPU资源的分时调度,进而实现cpu层面的多租户。
增大每个worker上处理的split数#
node-scheduler.max-splits-per-node参数。
类似于一次性取多少spilt数据过来。
元数据有配置支持缓存,避免频繁获取元数据,加快加载速度。#
使用Join语句时将大表放在左边:#
Presto中join的默认算法是broadcast join,即将join左边的表分割到多个worker,然后将join右边的表数据整个复制一份发送到每个worker进行计算。
