AQS和JUC核心原理
java-class类文件原理详解
java-object-in-heap
java常见容器使用原理(Map-List等)
java类加载全过程详解
Java线程池高级应用和原理分析
java编译优化和语法糖
jdk动态代理原理解析
jvm内存区域原理
jvm垃圾收集器演进和原理详解
synchronized关键字原理超级详解
volatile和CPU-MESI协议底层原理
java高级原理
java-base
java基础知识
随笔
java
心理感悟
java堆中分配对象的原理
Java对象在堆中的分配原理#
java对象new的一个过程
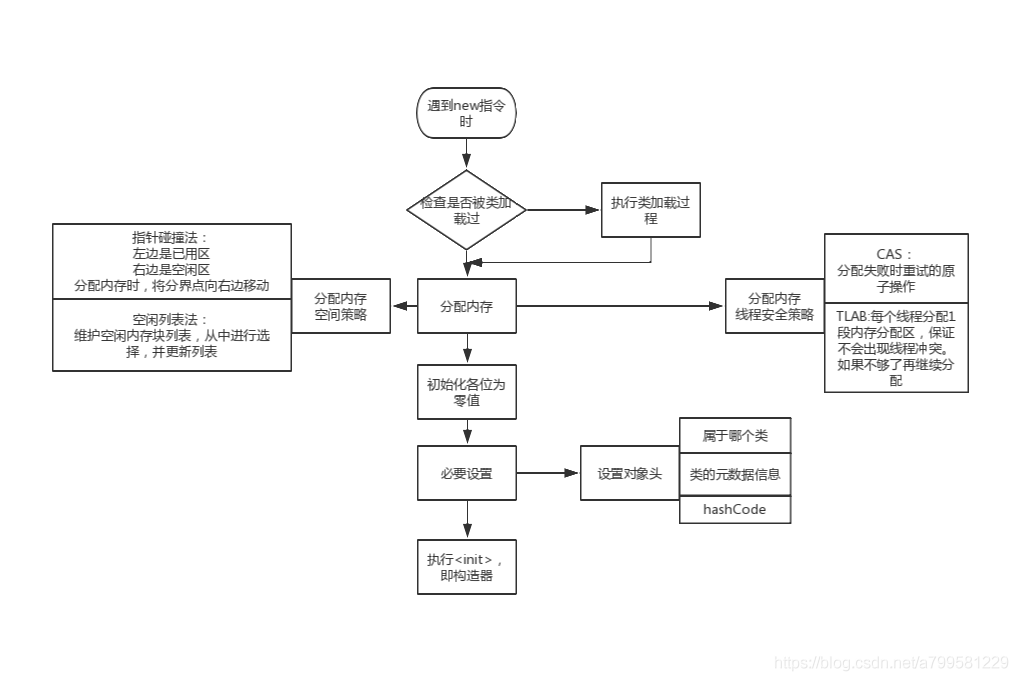
Q: 什么是TLAB?
A:
TLAB ——Thread Local Allocation Buffer
线程本地分配缓冲区
如果没有启用 TLAB,多个并发执行的线程需要创建对象、申请分配内存的时候,有可能在 Java 堆的同一个位置申请,这时就需要对拟分配的内存区域进行加锁或者采用 CAS 等操作,保证这个区域只能分配给一个线程。冲突概率很大
启用了 TLAB 之后(-XX:+UseTLAB, 默认是开启的),JVM 会针对每一个线程在 Java 堆中预留一个内存区域
一旦某个区域确定划分给某个线程,之后该线程需要分配内存的时候,会优先在这片区域中申请。这个区域针对分配内存这个动作而言是该线程私有的,因此在分配的时候不用进行加锁等保护性的操作
Q: TLAB给线程预分配空间的时候,如果多个线程竞争同一个预留空间冲突了怎么办?
A:
在预留这个动作发生的时候,需要进行加锁或者采用 CAS 等操作进行保护,避免多个线程预留同一个区域
Q: 分配的时候,在TLAB区域里,怎么知道放在哪个位置呢?
A:
具体的分配内存有两种情况:第一种情况是内存空间绝对规整,第二种情况是内存空间是不连续的。
对于内存绝对规整的情况相对简单一些,虚拟机只需要在被占用的内存和可用空间之间移动指针即可,这种方式被称为指针碰撞。
对于内存不规整的情况稍微复杂一点,这时候虚拟机需要维护一个列表,来记录哪些内存是可用的。分配内存的时候需要找到一个可用的内存空间,然后在列表上记录下已被分配,这种方式成为空闲列表。
java对象在内存上的分配:
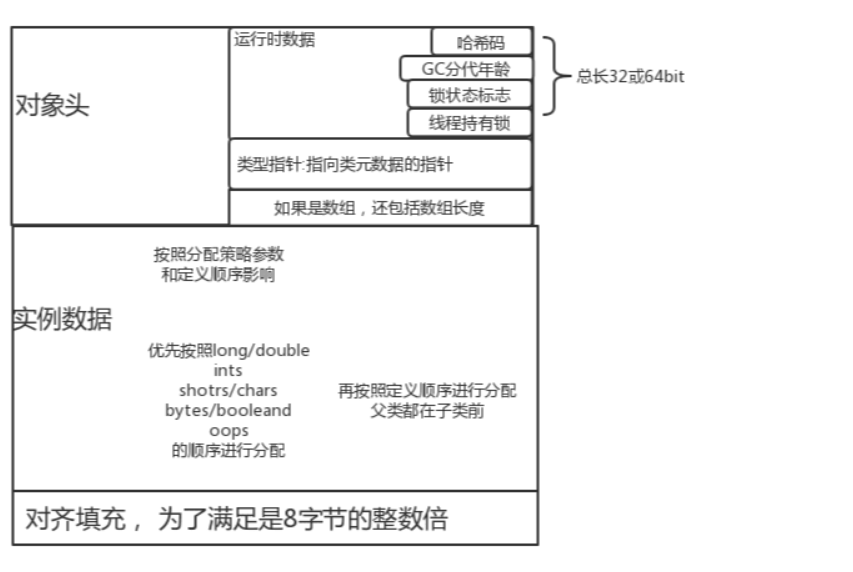
Q: 对象的hashcode确定是创建对象的时候生成的?
A:
不对。采用延迟加载技术
Q: 如何计算一个java对象大小?
例如下面的person?
1 | class People{ |
A:
这里假设使用64位机器,采用指针压缩,则对象头的大小为:8(_mark)+4(_klass) = 12(如果没开启,k_class即对象引用地址占8个字节)
然后实例数据的大小为: 4(age)+4(name) + 8(birthday) + 8(sallary) + 2(tag) + 4(引用,开启指针压缩) + 1或4(married) = 31 or 34
因此最终的对象本身大小为:12+31+5(padding) = 48 或者 12+ 34 + 2(padding) = 48
PS1: 注意布尔值可能是1或者4,根据虚拟机规范不同有不同,4字节的话好处是CPU
PS2: 注意,指针压缩不仅仅影响对象头,还影响了对象内的引用大小。
更详细的见如何计算Java对象所占内存的大小
Q: 对象头里的markword到底是啥?
A:
markword根据锁标记的状态,里面存储的了不同的内容。

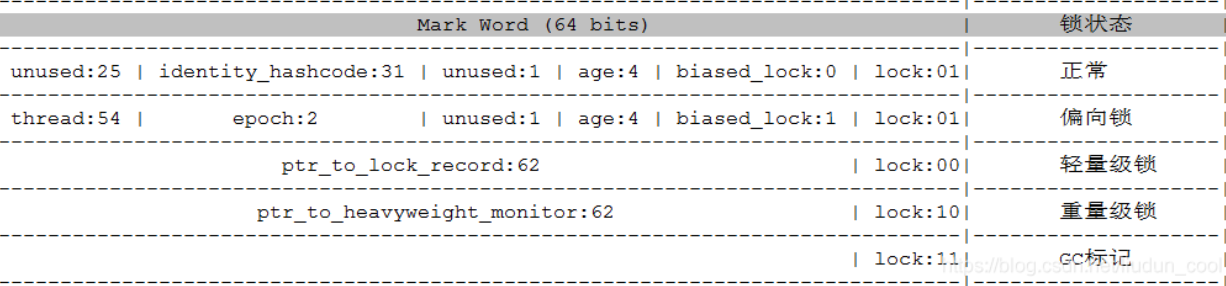
java对象头 MarkWord
Q: 哈希code 有锁的时候,hashcode又去哪了?
A:
identity_hashcode:31位的对象标识hashCode,采用延迟加载技术。调用方法System.identityHashCode()计算,并会将结果写到该对象头中。当对象加锁后(偏向、轻量级、重量级),MarkWord的字节没有足够的空间保存hashCode,因此该值会移动到管程Monitor中。
Q: 对象内存字节为什么要按8字节对齐?
A:
对齐填充是底层CPU数据总线读取内存数据时的要求
例如,通常CPU按照字单位读取,如果一个完整的数据体不需要对齐,那么在内存中存储时,其地址有极大可能横跨两个字
例如某数据块地址未对齐,存储为1-4,而cpu按字读取,需要把0-3字块读取出来,再把4-7字块读出来,最后合并舍弃掉多余的部分。这种操作会很多很多,且很频繁
但如果进行了对齐,则一次性即可取出目标数据,将会大大节省CPU资源。
另一种说法:
Scott oaks在书上给出的理由是:
其实在JVM中(不管是32位的还是64位的),对象已经按8字节边界对齐了;对于大部分处理器,这种对齐方案都是最优的。所以使用压缩的oop并不会损失什么。如果JVM
中的第一个对象保存到位置0,占用57字节,那下一个对象就要保存到位置64,浪费了7
字节,无法再分配。这种内存取舍是值得的(而且不管是否使用压缩的oop,都是这样),因为在8字节对齐的位置,对象可以更快地访问。不过这也是为什么JVM没有尝试模仿36位引用(可以访问64GB的内存)的原因。在那种情况下,对象就要在16字节的边界上对齐,在堆中保存压缩指针所节约的成本,就被为对齐对象而浪费的内存抵消了。
** 8字节对齐,是为了效率的提升,以空间换时间的一种方案**。当然你还可以16字节对齐。但是8字节是最优选择。
Q: jvm的指针压缩原理是什么?
A:
我们都知道java中的对象都是8字节对齐的,8字节对齐有一个特点就是总是加上1 000。 发现了吗, 所有对象的指针后三位总是0。这就是指针压缩的点。
压缩原理就是两句话:
1:存储的时候,后三位抹除0.
就变成:test1=00,test2=10
2:使用的时候,后三位补0.
它的指针不再表示对象在内存中的精确位置,而是表示 偏移量 。这意味着 32 位的指针可以引用 40 亿个 对象 , 而不是 40 亿个字节。最终, 也就是说堆内存增长到 32 GB 的物理内存,也可以用 32 位的指针表示。(4字节指针地址原先只能表示4个G的大小)
Q: 指针压缩什么时候会失效?
A:
因为寄存器中2的32次方只能寻址到32g左右(不是准确的32g,有可能在31g就发生指压缩失效)
所以当你的内存超过32g时,jvm就默认停用压缩指针,用64位寻址来操作,这样可以保证能寻址到你的所有内存,但这样所有的对象都会变大,实际上未开启开启后的比较,40g的对象存储个数比不上30g的存储个数
Q: 为什么对象头里的kclass也会受指针压缩的影响?class实例不是存储在方法区里么?
A:
JDK1.6中Class实例在方法区
JDK1.8之后, class实例本身就是一个对象,分配在java堆中。而class字节码加载后的各种细节内容则存储在永久代中。
HotSpot并不把永久代中的instanceKlass暴露给Java
而会另外创建对应的class对象instanceOopDesc来表示java.lang.Class对象(即这个对象里不会包含class细节字节码的内容),并将后者称为前者的“Java镜像”, 对象头里的klass就是持有指向类oopDesc引用(_java_mirror便是该instanceKlass对Class对象的引用);
Q: 在方法栈中执行代码时,如何通过引用定位到堆里的对象?
A:
两种方式,通过句柄池,或者通过指针。如下图所示
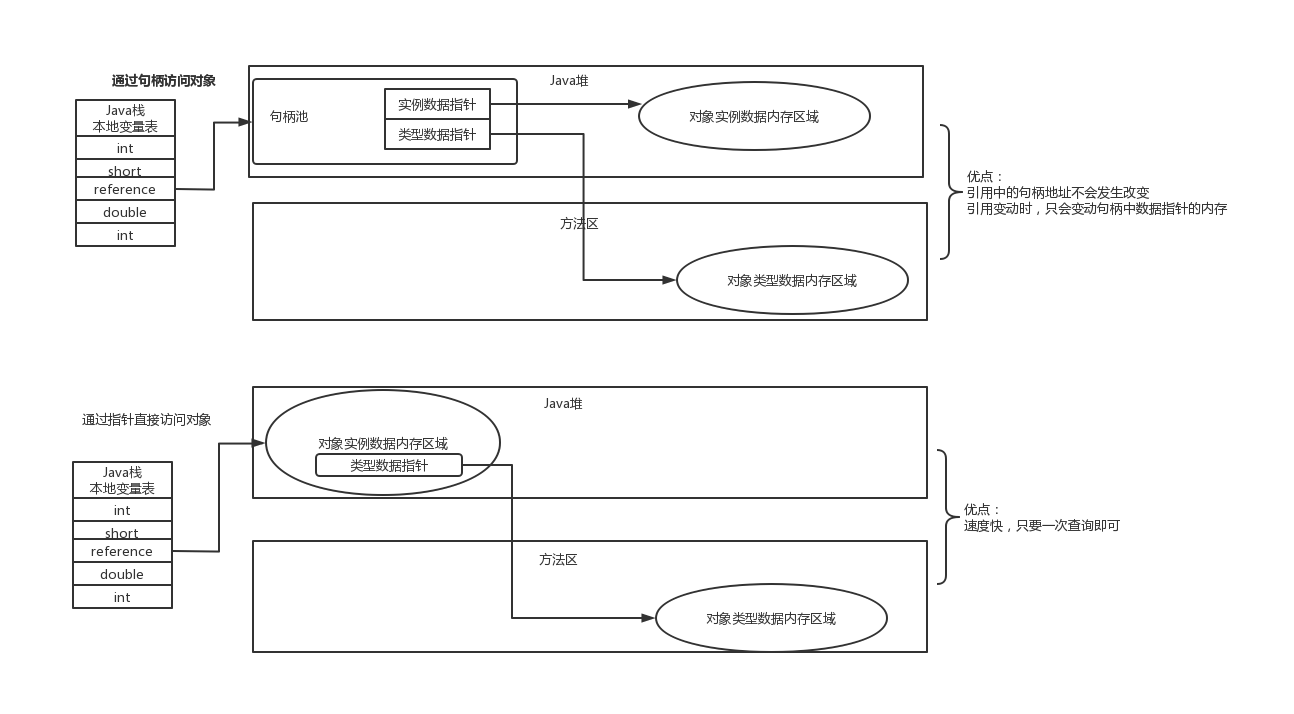
Q: 句柄和指针的区别是什么?
A:
句柄池, 引用中的句柄地址不会发生改变引用变动时,只会变动句柄中数据指针的内存
可以理解为,句柄池方式, 创建新对象后,句柄位置就定下来了。后面如果频繁修改引用, 只会修改句柄里的指针,但是本地变量表里寻找的位置都不会变化,因此不用经常跳到各种本地变量表去修改。
- 频繁gc、修改引用的,用句柄池引用
- 频繁访问固定对象的,用指针引用
Q: 怎么确认用的是句柄引用还是指针引用?
A:
sun HotSpot用的指针引用,速度快
访问方式,取决于虚拟机的实现。
Q: 方法里创建基本类型的局部变量时, 为什么不把基本类型放堆中呢?
A:
因为其占用的空间一般是 1~8 个字节——需要空间比较少,所以不会出现动态增长的情况——长度固定,因此栈中存储就够了,如果把他存在堆中是没有什么意义的。
可以这么说,基本类型和对象的引用都是存放在栈中,而且都是几个字节的一个数,因此在程序运行时,他们的处理方式是统一的。但是基本类型、对象引用和对象本身就有所区别了,因为一个是栈中的数据一个是堆中的数据
Q: 那我new出来的对象, 一定都在堆中吗?
A:
HotSpot虚拟机引入了JIT优化之后,会对对象进行逃逸分析,如果发现某一个对象并没有逃逸到方法外部,那么就可能通过标量替换来实现栈上分配,而避免堆上分配内存。
Q: 刚才new对象的过程,可能存在重排序吗?
A:
存在。
①「JVM」为对象分配一块内存M。
②在内存M上为对象进行初始化。
③将内存M的地址复制给singleton变量。
可以是「①②③」或者「①③②」。 这也导致了双重检查锁时,为什么有了sync还要加volatile。
但是另一种说法,是JDK高版本之后, 将这个new语句看成一个大号的volatile写,因此这个大号volatile写前后会有内存屏障,与volatile读隔离开来,因此虽然volatile读不知道大号volatile写的内部顺序,但是知道它的结果一定是执行完那三步的。
因此重排序仍然存在,但是会特地限制其他对该对象的new的过程是有屏障的。
Q: 上面的过程的指令码是什么样的?
A:
1 | 0: new #16 // class jvm/fenixsoft/DynamicDispath$Man |
那么为什么要进行备份呢?
一开始是new指令在堆上分配了内存并向操作数栈压入了指向这段内存的引用
之后dup指令又备份了一份,那么操作数栈顶就有两个
再后是调用invokespecial #18指令进行初始化,此时会消耗一个引用作为传给构造器的“this”参数, 注意这个指令会将栈顶的引用拿走,因此dup指令都是用于这种场景的,即栈顶的引用存在消耗。
那么还剩下一个引用,会被astore_1指令存储到局部变量表中,后面调用的代码会用到。
【反八股系列】一、为什么我们要学习java虚拟机栈的原理?
曾经的八股文:
xxx
现在的八股文:
xxx
为了找回对编程最初的乐趣
决定自制反八股系列的知识视频
本系列的三大宗旨:
拒绝死记硬背
拒绝管中窥豹
拒绝浅尝则止
对于jvm的虚拟机内存结构,大家应该都能背会有“2个堆”、“2个栈”、“1个计数器” 这种内容,就像下面这张图一样。 其中java的栈是虚拟机指令执行的关键。
那么,为什么我们要学习背后的这个虚拟机栈呢? 我的代码能跑起来不就了可以吗?
哦,是面试要用么?然而个人不希望这些内容成为新一代的“科技八股文”。
因此本系列希望先从为什么学习入手,再深入到更深层次的东西,,希望能带来的是长久的收获,而非短暂的记忆。
为什么我们要学习背后的虚拟机栈。
首先,你debug的时候,你都不知道这个是什么东西,瞎猜可不行,你要知道暂停时现在是个请什么情况, IDE上的东西到底是什么,他们对程序运行又有什么影响
[debug图片]
其次,虚拟机栈的内容是很多重要知识的前置知识点。 垃圾收集的GC-ROOT与栈有关, JIT优化和栈有关。如果你不知道,那么在遇到相关知识点,只会产生“这是啥”、“这又是啥”的连锁反应, 就有可能陷入背诵八股文的折磨却不知所以然的地步。
最后,java虚拟机栈为我们生动展示了 一个小心的迷你的CPU执行逻辑。
对于很多没有学习过计算机底层原理(例如CSAPP这本书) 的人来说, 是完全不知道计算机是如何执行机器码指令的。 而java虚拟机栈可以更好理解 指令是如何运行的, 虽然这个指令不是真正的机器码执行, 而是jvm字节码指令。 但是通过字节码指令, 我们可以快速对应到java中常见的各种操作。
这对于很多入门时直奔删减改查的同学来说, 是不可多得的学习底层的机会。
另外数据结构里学习的栈的知识也会在这里得以应用。
清楚了上述好处后,我们开始深入了解虚拟机栈的细节。
首先,栈帧是什么?
不需要去记忆概念,就记得我们调试时,框框里的每一行,就是一个栈帧。 可以看到除了栈顶的方法正在执行外, 其他行都仿佛静止了一般, 因此就像拍照时的一帧。
对于栈帧里有什么, 经典背诵4件套:
局部变量表,
操作数栈,
动态链接,
方法返回地址,
其实与上面这4样配合的,还有个虚拟机栈所使用的“程序计数器”,才共同实现了jvm指令的执行。
首先对局部变量表而言, 为什么要有这个东西?
5 4 3 2 1 .
因为我们声明的局部变量a、b、c等, 都需要有一个地方存放, 但局部变量只有这个方法中才会使用, 所以才会在栈帧中开辟局部连量表的空间。
那么,变量表有多大呢?
编译时指定定死了
为什么能定死?
因为编译器很聪明,通过分析代码,他就能知道到底这个方法要用几个变量。
为什么我们需要思考这个问题?因为我们要考虑我们写的代码,可能会带来多大的局部栈的消耗。
例如,我在一个for循环里反复定义同一个变量,那局部变量表是不是在无限增大?我是不是要提前加大栈的分配内存?
其实不需要, 因为编译器支持变量表的复用, 它会知道你在重复声明变量,所以实际字节码指令中,它会明确写下“这个变量继续放到前面那个槽”的指令, 从而覆盖使用了之前的槽。
你问我怎么分析的? 请阅读《编译原理》。
然后操作数栈又是干什么的? 如果要做a+b,我直接从变量表上取a的值和b的值,加起来不就好了?
直接让CPU取a和b的值拿去算完回来,不就好了?
那我如果是 a + b*c呢
b*c的值放哪里?
如果是a+b*(c+d)呢?
这时候如果你学习过数据结构里栈的应用 ,就会知道 模拟一个计算器,往往需要一个栈。
而操作数栈就是这个作用。
当你学习jvm指令时,就会看到有专门的指令就是取栈顶或者把值推送到栈顶的指令。
这样做加法的时候,也就不用关心变量的地址了,只要你把栈顶的值存好,我直接拿去加就行。
那么动态链接又是个什么玩意?
就这么说, 你怎么知道这个方法此时要做哪些动作?
肯定有一段代码区(即jvm指令),让我一条条执行对吧?
那么这个代码区放哪呢?我总需要知道一个地址, 因此,动态链接,就是这个方法代码的位置。
那干嘛叫动态链接这么抽象啊?
因为有的方法往往是等运行的时候才知道地址, 所以统一就叫做动态链接了,这就是未来会提到的java多态的核心本质而。
那么返回地址比较好理解,方法执行完成, 返回上一层方法执行的位置。
等等,这个地址是实际的地址吗?例如0x2313212这种?
应该是把,不然怎么叫地址?
但是我已经有动态链接标记的方法指令的起始位置了,你为什么还要整这么长?
哦,那就用偏移值就可以了!
那现在再看,程序计数器,代表的是什么
很显然和方法返回地址一样, 也是指令偏移值, 这样通过动态链接 + 计数器, 就能知道这个方法当前执行到什么位置了, 即使发生了线程切换或者方法返回, 都不用担心了~!
那么再深度扩展一下,根据以上理解,是否能清楚下面这个的原因代码的原因
当你知道远离后,你就不需要记忆这种情况,而是一想背后的实现,就能明白这么写是不对的。
1 | public class Test { |
就是在执行 finally 语句块之前,try 或者 catch 语句块会保留其返回值到本地变量表(Local Variable Table)中。待 subroutine 执行完毕之后,再恢复保留的返回值到操作数栈中,然后通过 return 或者 throw 语句将其返回给该方法的调用者(invoker)
因为你要处理finally块时, 操作数栈要腾出来给finally使用, 因此返回值不能放在这,所以整了个局部变量ret放进去, 执行完成返回来。
21年10月-22年5月
[toc]
刷题日记
😉 😢 😆 😋
[2022-05-09]
- 给一个图,找入度为n、出度为0的唯一点,最少可以通过3n次查找,从0到n通过遍历a->b,逐步排除不可能的选项,最终只剩1个,然后再通过2次n确认入度和出度。 😄
- s.indexOf(i, “}”) 可以快速得到下一个
- 要求ty通过反复减tx,要减到小于等于tx的话 那么就是ty%tx的值
- 对于自己推导中间过程比较麻烦的题目,就直接写个sout打印中间能很快观察到问题所在
- 先写个超时的答案
- 打印中间结果,看下哪里浪费了
- 对浪费的步骤做优化
- 求1个数字N是否为质数的一个简单方式: 只遍历i=2到i=根号(n),然后确认能否被整除即可。
- 优化1: 求二进制1的个数,没必要手动求解, 直接用Integer.bitCount()即可
- 优化2:质数如果总数比较小,可以直接手动大表,这题里最大数字范围为19 ,那么质数可以直接打表得到
- 找到一个最小高度的树的根节点,可以用拓扑排序,从最外围往内部逼近
- n如果是整数,可能直接越界,需要提前强转
- 如果状态条件种要求不能连续的问题, 考虑状态是否多加一个,这题的状态方程就是,dp[当前位置][颜色][上一个点是否是该颜色]
- 知道很多点的大小关系,求整个的大小关系,可用拓扑排序
- Stringbuilder.reverse() 会导致自身翻转,所以切忌不要对搜索变量stringbuidler做翻转,要么记得转回来
- 如果二进制a都是0、1交替的,那么a ^ (a>>1) 则会变成除前置0外,全是1
- 如何判断某个二进制a全是1组成?a&(a+1)==0, 则说明全是1
- 多个字符串编码成1个字符串,可以用非ascii码的字符做分隔符(char)257
- 涉及次数问题的题目,且题目次数一定小于某个总数,则可以考虑计数排序
- 涉及数字出现次数,求里面某几个特别的次数的数字时,记得使用分类,即想办法把他们分成不同的组,再分别做异或即可。
- x&(-x)是x=110100变000100, x&(x-1)是x=110100变111000
- 如何判断一个图是否是1课树?
方法1:首先保证边数=节点数-1,然后用bfs保证所有点相连
方法2:并查集,合并过程不能出现2个根节点相同(说明树内循环连接了),合并完成要求只有1个根节点
- 一个数组,如何求去掉每个位置时的数组中的最小值
维护最小值和第二小的值即可
注意,当更新最小值的时候,同时需要更新第二小的值!
- 自定义迭代器注意点:迭代器特点,无论是hasNext还是next,都需要先找到下一个有效的点, 再去判断,而且是通过while循环查找。
- int[] 截断成list,可以先转list,再用subList截断.
ret.subList(0, k); - 寻找num在list中的位置:Collections.binarySearch(list, x);
- 用常量空间判断数组是否是二叉搜索树的先序?
遍历每个点,只测试右边方向的正确性
*1个有序数组,求2个数字的和满足target,可以用双指针最左和最右,然后根据大小情况移动左边或者右边。为什么不可能往回走?因为你之前已经走过的点,能确认右边那个位置是无法满足的
- 中序遍历迭代树, 注意走下一个点时,要么右儿子为空往上走,要么走右儿子后,还得往左边一直走到底,才算是下一个点
- list[]初始化,直接for循环最简单
- 一个java-stream的小点: 按照key分组并统计每组key的数量
Map<String, Long> strMap = Arrays.stream(strings)
.collect(Collectors.groupingBy(s -> s, Collectors.counting()));
即groupingBy(key->key, Collectors.counting())
如果记不起来,马上改成用stream().foreach或者直接循环即可
- 2个单词在词典中的最短距离,最好方式是用双指针,如果i1<i2,则i1++,这样子
- unicode形式的字符,尽可能用character对象,一个字符可能是多个字节表示,因此不能用数组下标来简单处理这类字符的哈希问题
- 如果求解二叉搜索树的第k个点,要求频繁查询的性能,则事先统计每个子树的节点总数量,即可快速判断在左边还是右边。(如果不平衡则要平衡树)
- p、q最近公共祖先问题,可以不一定用父亲数组遍历2次, 而是用 该树是否包含p或者q的布尔值结果,通过先序遍历,找到第一个左右两边都有p\q的情况(也包括自己是p或者q)
- 如果希望使用双端队列而不是栈,请不要用Push和poll了,就用first和last两个语义处理,避免混乱
- LinkedList push 施加在list头部. 等同于addFirst。 add 是加在list尾部。
- 如果一个式子中只有+号和-号,无括号,则直接将-号后的数字取负即可
超期优先队列应用
- 如果题目只需要你返回true或者false,即不需要中间所有结果,则考虑到一些情况可以不用过分担忧,如果有影响,则可能直接返回true了
- 完全二叉树的节点是否存在,可以用位运算来表示,往left走代表0,往right走代表1.
- 回文串最简单的判定s = 翻转(s), 可以考虑字符串哈希等东西,或者KMP前缀后缀判定优化
- 字符串哈希,第0位数字不可为0,至少要有数字,因此不需要做s.charAt(i) - 'a’的操作
- 因此股票买卖,要考虑持有或者不持有,然后通过买入扣钱以及卖出加钱来计算
- 字典树问题,如果是考虑单词“全匹配”,则必须要在字典树末尾补充isEnd标志。
- 字符串只有10时,做substring和map.hashcode的时间都是可接受的,可直接用
- 子序列对应x进制的滑动窗口问题中,你可以先整体右移动,然后截断第一个位,再加上最后一个,即可。
- 如果窗口大小是的2的倍数,则可以继续用位运算,只不过偏移数量要变化

- 对于长度固定的窗口,你可以先预处理窗口剩1个, 然后再开始,避免重复判断

- 如何O(h高度)遍历二叉搜索树? 利用栈,每次把左左左放入,然后出栈时,右儿子放入后继续左左左放入
- 几个数字怎么排列乘一个数字后最大, 只要满足a+b>b+a,那么a就放在前面即可。
- 字符串去除前置0的操作:.replaceAll(“^(0+)”, “”)
- 字符串a+b和b+a做比较觉得不好,可以改成long整数,分别乘高x10位加另一个数字来比较
- 一个节点的祖先和后代节点集合, 一定包含在他父节点的祖先和后代节点集合
- 可根据各节点的祖先和后代节点数量,确认是否是祖先关系,父亲节点是数量最靠近自己的
- 后面暂时不做每日一题了,直接按面试高频题进行练习。
- 注意javaStream.filter中,是满足条件的留下, 而不是剔除。
- 边界比较麻烦的问题,要自己写一下UT用例,覆盖边界场景,再写代码,这样就算错了,给人留下的印象也会很不错
- 快速计算list或者map.values()的最小值方法:Collections.min(collection)
- 滑动窗口遵循下面的写法最简单:
- 只写一个while循环,即只默认循环加right
- 每次都直接把right放入窗口。
- 当窗口不满足,则移动左节点直到满足。如果左节点大于右节点,结束左节点的移动。
- 计算当前窗口结果。左大于右时,要能算为0
- right++
- 求List
的int最大值时,需要先mapToInt, 再求最大值。 如果最大值可能不存在,要用orElse设置默认值 - 分子/分母的整除对象做哈希键时,需要做4种处理
- 分子必须保证为非负数(如果小于0,则上下都乘-1即可)
- 需要求出gcd进行最小约分
- 用最大边界来表示这个二维值:(分子/gcd) * 最大边界 + (分母/gcd)
- 分子为0,那就简化成(0,1), 分母为0,那就简化成(1,0)
- 每次提交代码前,必须看一下中间10^5范围的中间结果是否可能超出int范围。
- 对链表题排序, 注意每次排序完部分链表时, 需要更新最后一个节点的next!
- 如何对链表做排序,且空间复杂度最小?使用迭代法的归并排序,即自底向上的归并排序。那么就很容易了
- 怎么划分2个需要合并的列表?提前把尾部设成null
- 合并两个链表时,可以弄一个局部头节点,这种不算空间复杂度,因为是局部变量, 后面会释放掉。
- 无法搜索的博弈论问题,尝试找规律, 当先手选某一步,之后大概率会陷入某类循环中,直到出现胜负。
- 不能很快得到公式时,不妨写土方法遍历1下看能否满足循环序列。
- 短时间想不到的博弈论问题,直接放弃,博弈论还是比较脑减急转弯的
- 如何避免构建初始滑动窗口的麻烦?可以往右边遍历时,到达某一个边界,才开始删除,就不用构建初始窗口那么麻烦了。
- 用迭代模拟递归核心原理:
- node局部变量,指代dfs方法中的node入参。
- 当前node还有用,但需要往下搜索时,把自身入栈,再更新node局部变量。
- 当stack.pop时,说明已经从dfs(left)或者dfs(right)中走出来了。 则按照递归代码,选择继续走right入栈,还是直接打印自身。
- node=null指代什么?指代必须要用stack.pop,即开始回溯了。当你试图回溯时,不可自己做node=node.right的操作, 而是要通过stack.pop处理
- 因此动规适用于单个结果,不适用于动规路径或者排列。如果需要求路径组合或者一定条件的排列组合,请使用记忆化搜索而不是动态规划。因为记忆化搜索时,只有成功搜索到底部,才会得到记忆化结果
- 链表首尾不断相连的解法: 如果涉及从后向前处理的链表,考虑反转链表再操作。 对于中点,使用快慢指针。
- 感觉不好计算最终数组有几个位置的话,不如直接用list,最后toArrya(new xxx[0])即可
return results.toArray(new String[0]); - 问题是分配问题,但是却需要你计算一个某最大长度结果,则可以考虑二分法,固定最大长度,再分配。
- 位运算问题,可以考虑“各位的数量",例如只有1个数字是1个,其他都是3个3个出现,那么可以从每位的1的个数,推断出那个数字(其他肯定要么是1的3倍或者0倍,加起来)
- 上一个状态集合是[00,01,10,11],和数字[0,1]碰撞后,得到一个新的状态集合[x,y…],则可以画出一个卡诺图, 上一个状态集合看作a\b两个门, 数字[0,1]看作c这个门,从而得到a和b的新状态电路情况

- 有时候要求满足复杂规则情况下,求最优结果,则可以考虑拆分成多种规则,取每个位置的最大值或者最小值

- 当从i往右滑动到j时,整个过程要求都满足区间和[i, k]大于等于0时, 一旦有[i,j]不满足, 则[i,j]中的任一点都无法作为起点, 因为[i,i]肯定满足>=0,则[i+1,j]肯定变得更小了,以此类推(或者说[i,xxx]这个前缀和肯定都大于0,得到中间任一位置都无法满足)
- 根据障碍数n,计算出一个能围住的最大格数max,如果a能bfs搜到的点大于max,说明没围住。 如果小于,则肯定围住了。
网格中,障碍个数n能围住的最大格子个数max= n*(n-1)/2 - x=1000000,y=1000000, xy不会超Long, 但是(x+1)(y+1)可能会超
- 差距某个字母才算相邻的单词相邻问题,可以使用虚拟节点求解。(同理可以作用到数组相邻问题上)
例如abc可以和bc、ac、ab*这三个虚拟节点相邻。
其他一样处理, 这样就可以直接连起来
还要维护id到单词、单词到id的2个映射map。 - 双向bfs可以降低空间消耗,但是不能降低过多的时间复杂度
- 力扣不支持bigInteger。如果在35位范围内,可以尝试使用Double表示大整数。如果长达几百上千位,就只能自己写string大整数加法了。
- 力扣竞赛,示例的正确答案在右边,不要看错了
- 可以先写一些用例,在跑,减少罚分,养成习惯
- 给你一堆固定长宽矩形的左上顶点, 让你判断某个点是否被任一矩形包含,则 可以反向前缀和, 求这个点的左上矩形区间内是否包含矩形顶点即可
- 前缀和别写错,注意要-1的都是左上角顶点坐标

- 组合数C(n,m)可以用杨辉三角求, 杨辉三角的n行m列等同于C(n,m)
- 遍历小写字母, 用for(c = ‘a’;c<=‘z’;c++)而不是for (j = 0; j < 26; j++) { (char)(j+‘a’)}
- 能用spilt分割就用spilt,别自己分割,容易搞错
- 当给树添加新的指针,让你做常见遍历,却要你用常数空间时,一定是利用新指针当作线索来做遍历,避免了用栈或者队列。
- 树的搜索, 用迭代替代递归的关键点:
- node局部变量等同于dfs(Node node)里的node入参
- while(node = node.left) 等同于走dfs(node.left)
- 取栈顶, 等同于if(node==null) return的这个边界
- node.right 入栈, node = node.right 等同于dfs(node.right)
- 要求空间复杂度为1的树中序遍历, 考虑利用左子树的最右节点的right空闲指针,指向自己,来快速跳转
- 二叉搜索树寻找问题节点, 直接遍历得到list,然后排序,就能找到问题节点了。
- 矩阵最大面积问题,提前想到单调栈,固定自身高度h,左右扩展。
- 计算星期几、日期相关题目, 统一用减去1970年12月31日的方式,拿到时隔多少天, 用天数去判断
- 子集问题,直接dfs,不要想着骚操作搞for循环,太容易写错了。避免重复,就是那个原则“必须连着选相同的,不能跨着选相同的”
- 如果是单调栈的题目,最终肯定只需要使用栈头的元素。 如果你发现需要遍历栈中所有元素,导致高度和宽度全在变化导致无法计算, 可以看一下是不是改变计算思路,固定自身为某个高度,而不是去寻找前面的某个高度。
- 把上一组n阶的格雷码集合 都在头部加一个1, 然后倒序加进来即可。(可以理解为先头部加个1跳进去,然后反向走一遍,就肯定能保证走回去了)
- 不要看到总数为n,分组长度最大为n,就认为自己的双重for循环可能有O(n^2)的复杂度。
对于会提前结束/退出判断的情况来说, 双重for可能最多就O(n),循环就会结束了
- a+b+c=d的等式问题, 可以转化为a+b=d-c问题
- 4个点的复杂滑动窗口问题, 可以只滑动中间点, 左边当区间复用历史结果, 右边做遍历。
- 从某序列变成某序列的“最短编辑距离”问题, 可以考虑动态规划, 判断从子序列A变成子序列B时,能通过做哪些动作实现部分匹配,再判断剩下子序列a和子序列b的最短距离即可。

- List<int[]> result如何转int[][]? result.toArray(new int[0][0]);
- 问你某某走法的数量,却要求空间限制,无法动态规则,则考虑组合数。
- 组合数快速解法:
1 | C(8,3) = 8 * 7 * 6 /(3 * 2* 1) =( ((((6 / 1) * 7) / 2) * 8) / 3) |
- 当数量很大,但是数值范围很小,却要你做二分、排序或者区间统计时,优先考虑直接用数组做计数排序/计数前缀和。
- 快速只保留末尾的1,其他全置0: b &(-b)
- 快速剔除末尾的1: b &(b-1)
- 全排列问题, 直接搜索每个位置能放谁,从0开始遍历+vis数组
- 重复问题的剪枝:只能连续插入重复的数字,不能跳跃着放重复数字。因为跳跃了的话,前面完全可以搜过一样的情况
- 遇到特定长度的子串/子数组是否重复/已存在的问题,可以考虑用字符串哈希
- 二分的最大right记得想清楚,不确定的话直接Integer.MAX_Value就行
- 问你最少替换几个数字, 可以变成递增序列, 其实 可以变成“求出最长递增子序列后, 剩下的就是要变的数字”。 或者说替换几个东西,可以变成xxxx, 是否可以改成求 最长的xxxxx,然后剩下的就是要改变的东西
- 如果设计key-value的value二分, 不要试图用treeMap,因为treeMap是基于key排序的。 做更新操作会恶心死自己,不如直接基于key二分,然后判断value
- 数独判断的问题记得先写针对区间的check函数,再判断,会简化很多操作。

- 旋转数组二分问题,每次找有序的那段,再去判断
- 旋转数组如果有重复数字,提前处理左右边界都相等的情况,都+1和-1,这样就省了很多复杂场景了
- 滑动窗口求最大值问题时,不要忘记求初始窗口时的最大值更新。
- 排序过程如果涉及索引,可以考虑弄一个索引i的数组,对i做排序,不需要带着索引弄个二维数组很麻烦
- Arrays.sort如果要对int[]数组自定义排序, 应该使用Integer[]而不是int[]数组。
- 如果滑动窗口如果发现删除点的操作比较麻烦,可以尝试事先利用数组特性预计算一些前缀和等数据,提前算好那个区间的值,而不需要去考虑移动时点的更新。
- bfs时,一定要记得第一个入队的点需要设置vis[x] = true,这个很容易漏!
这下面的是从旧往前, 而最新的都改成了新的放上面
- 复杂字符串解析问题, 尽可能避免边解析边计算,可以分成2步来做,先解析成N个字符串,再依次判断和计算。
- 并查集问题,涉及边界相连的情况,可以将边界认为是一种集合。
- 二维点问题,尽可能用index = getIndex(y,x) 获取二维索引, 避免大量二维数组操作, 用InArea(y,x)方法减少判断代码。
- 相连、成环问题,都要想到可能和并查集有关
- 对于复杂的模拟过程题目,一定要自己在纸上把几种情况列出来,切忌脑测然后想出一个完全不合理的解决思路。
- 字典树的使用和查询过程,切忌偷懒,不要漏了走到null节点结束查询的情况。
- 迷宫理论: 总共n种位置,走了2n步,则一定是死循环,无法走出(在博弈题里即平局)
- 动态规划,记得步长或者回合数是可以当状态的, 不要漏了这个,不要死脑筋只想着做状态压缩
- 位图状态压缩,力扣题几乎都是16位情况的压缩, 几乎不会出现32位以上的,超过这些,则考虑是否可以不需要记录走过的点之类的。
- 一组数字,如果只能加和减任意x,且要求最终相等, 他们必定互相之间的差值是x的倍数
- 求和问题、绝对值问题,注意最好先自己用数学公式推导一下,更容易快速理解思路,切忌胡思乱想
- 交替复制的问题,可以使用双指针来做
- 优先队列:a是上面的点,b是下面的点(儿子节点),(a,b)返回大于0的时候,则交换
- 涉及排序变化,由数组A变成数组B的问题, 确定一下是否存在 ”稳定排序“,即不会跨相同数字变动, 能确定的话,就可以确定数组B中每个数字是由哪些位置的数字变化而来, 从而找到突破口
- 什么情况下Arrays.stream(数组)之后不需要boxed()? 即不是int[]、long[]这种需要转包装类型才能变成list的情况
- 记忆一下.collect(Collectors.toList()))
- 滑动窗口, 建议先用for循环移动右边, 确定右边的位置后,再用while移动左边找到满足条件的左边界, 这样可以简化很多判断

- 数组A和数组B个数相同,B里的每个值要通过+1、-1变成A时,需要的次数为 ”AB分别排序后,每个i位置的Math.abs(a[i] - b[i])总和“
- 即使心态不好, 也要仔细审题加看例子,不能不理会用例,错过用例很可能就理解错误导致gg
- 边比较少点比较多的情况时,如果要求最短路径, 则用bfs,不需要djkstra
- bfs求最短路径时, 只需要newDis < dis[node],再入队即可,且不需要做很多的vis判断。记住这个bfs求最短路

- n个数小于16的时候, 如果题目涉及选或者不选,那么是可以直接暴力枚举出所有的情况的,不需要用dp缓存之类的。
利用下面的代码求某一位怎么用上,不需要vis数组或者while除2啥的很麻烦的那种
1 | for (int j = 0;j<len;j++) { |
- 某DAG点如果可以重复走,那么当你走到某个位置时,其最小路径和次小路径已可以在出现后确定,后面的情况斗则可以不用考虑。
- 字符串日期天数问题,可以直接取一个基线例如1971年来计算天数。
- 快速将map的key变成list的方式, 注意记忆.collect(Collectors.toList()):
1 | List<Character> keyList = map.keySet().stream().collect(Collectors.toList()) |
- 树的层序遍历打印不一定要用bfs, dfs也行的,就不用存object[]了。
- 下次碰到复杂单词校验,如果正则忘记了,则直接上状态机,会简单很多。
- 状态变化设置不要放在枚举的构造器里做,初始化可能会出现null,如果顺序不对的话。放static块中做
- 注意Arrays.stream()不支持对char[]操作。
- 当遇到答案是乘起来或者很多数字加起来的时候, 最好直接改成long做计算,避免溢出。
- 链表转换题中,注意如果left和right会变化,则你原本想递归的东西可能会变动, 因此要提前缓存
- Math.ceil() 可以实现向上取整, floor向下取整
- Math.log可以求 Math.log(a) /Math.log(b) 等同于loga(b)
- 教训: 深度搜索时, 主要先确定层级,如果有n个东西必须做某件事,那就拿这东西做层级,中间for循环搜不同情况即可, 东西搜完了就说明符合条件
- 注意,涉及按时间在图上走的情况,是可以制造一个三维的图(数组),用时间做某一个维度即可避免冲突或者搞乱。
2021-11-21
- 遇到边界问题很难受,不知道-1还是-0的,自己冷静下来模拟一下
- 1-9有9个1位, 10-99的有90个2位, 100-999有900个*3位, 问你第1000位是1-∞中的哪个数字。
这时候冷静处理闭上列出来 9个 180个 811个
811个中,分别是 100 101 102 103
让序号从0开始,则811-1 = 810, 然后用除法和取余即可。 - 注意要用到取余判断某位是什么时,记得序号从0开始
2021-11-22
- 洗牌算法: 数组0-n,每次对n随机取余后,将对应位置的数字交换到最后一位,然后减少n,继续操作。
- rand.nextInt()的范围是负无穷到正无穷, 如果rand.nextInt()%M, 则范围为-M 到M。 因此应该改成rand.nextInt(M), 则范围为0-M-1
- stream中join的用法:.collect(Collectors.joining(“,”)), 而不是直接join
- 环形数组如果要求避免头尾相碰, 可以选择去掉头或者去掉尾,做2次, 就能不考虑环的问题了
- 动规、个数问题,优先考虑 dp[从i到末尾][某条件] 而非用区间去判断
- 树的左边界、叶子、右边界问题, 如果时间紧急,用3次遍历解决即可。 如果追求代码精致, 则用2个标记,不断往下传递,根据情况变化,需要自己考虑好边界条件,慎用。

- 如果要求在10000*10000的数字中进行多次不重复的随机选取, 内存不够的情况下, 可以利用map映射,将已被选的数字和末尾数组数字进行映射。

- 最大最小值问题,一定要注意如果最大最小是同一个值的情况
- Math.abs(a-b)-1 误写成了 Math.abs(a-b-1), 绝对值计算一定要注意-1是不是写错位置了
- 带条件的并查集(即满足条件才能相连), 应当按时间顺序做尝试性连接, 连完后发现不符合条件,则要重置该节点的parent,避免后面连错。
- 并查集结果返回时,返回前的判断应该是 findParent(node) 是否满足而非parent[node]是否满足, 因为可能还没做压缩。
- 迭代法前序遍历树: 往栈里放儿子时,直接倒序放入即可。
- 如果前面的信息可以利用,则考虑用滑动窗口,减少空间占用。(删掉一个元素以后全为 1 的最长子数组)
- 原地矩阵置0问题, 考虑用第一行和第一列来做临时存储,然后用标记变量判断第一列和第一行是否需要置0。
- 数字不相邻排列问题,按数量从大到小插入,插入时先偶数位插入,再奇数位插入,则一定保证题目要求
- 统计子串中的唯一字串。碰到某些问x唯一的情况, 想办法从x的角度出发找唯一的串或者子序列。
- 想不到的时候,试着换一个维度去,原本是从a推b, 看下能否从b推a
- String自身按照字段序重新组合方法:
1 | char[] cs = str.toCharArray(); |
- bfs题,注意y\x\ny\ny不要写错,每次写完检查一下

- 求最长回文子串, 注意 i和前面某中心的对称节点j, 则j的回文长度信息是可以进行利用的。
- 全排列不一定要用dfs去搜索。因为 第4位时,它的可能性就是前面3位的可能性总和再拼上第四位。因此一直记录当前result全集, 然后走到第x位时,让第x位和result全集拼接,再生成一个新的result集合
- k的子变量不要用kk, 同理不要用ii作为i的自变量, 很容易写错, 应该是indexK之类的,做到第一位不同,否则很容易写错。
- 如果本来是可以利用哈希表,但要求原地算法的题目, 则可以考虑用数组本身作为哈希表
- 数组迭代期间不要试图取更新数组值,因为更新的话迭代的nums是会变的,并不是不变的。
- 涉及运算符的题目, 用switch+string的特性即可, 不用搞OP枚举,太容易错了
- 二维场景加?:表达式很容易漏加括号

- 二维场景如果不想加边界判断, 可以用这种扩充边界思路, counts设置成 counts[m+2][n+2], 然后坐标从1,1开始即可。
- 简单题如果发现要很麻烦的dfs时,直接看下数据范围,确认能否从全集上去直接计算结果,而非从搜索去推导结果。
- 求公共祖先或者树点到树点路径, 除了向上求祖先之类的外, 还可以用前缀法, 即求出根到2个点的路径,去除相同前缀即可。
- 给一堆边,让你把他连成一条线(一笔画问题),且题目保证有借, 则考虑这是欧拉问题。 起点和终点是能明确的,直接用Hierholzer算法求。 具体见欧拉路径
- 即需要边搜索边删除’边’的情况, 可考虑存储边的迭代器引用后,再进行搜索
- 括号的全排列问题, 可以用 (a)b的形式去利用a、b缓存逐步求解,不需要dfs
- treeMap的floor 和celling总是记不清, floor——浮——水—— 要找的值在水上,但是只有下面的水key
- KMP算法的本质是[前缀-后缀]匹配算法, 后缀不匹配时,快速找到之前匹配部分的前缀位置。
- 是否可按线性跳跃到某点的问题,如果发现从后往前不好判断,会超时,则试着从前往后,根据当前最远到达位置判断, 有点类似于bfs。
- a+b>c时如果a+b可能溢出,则改成减法 a>b-c
- 不要做这种map.get()==map.get()的操作,高危操作。 Integer的==是引用。 要用equals。
- 滑动窗口中的个数匹配问题,用下面这种if-else去判断是+1还是-1。
