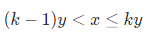只记录一下对我而言比较有意义的题目

本期总结：#

1. 遇到类似坐标 j - i == nums[j] - nums[i]的题目，记得直接转移公式以期望得到一个f(x)从而建立基于f(x)做key的hashmap， 不要想着什么从左往右+多少减多少这种绕来绕去的思路。

2. 数字num要拆成任意个比Target小的任意数字，且还要拆后的最小值尽可能大，那肯定不是直接基于target去做减法，而是让数字尽可能平均， 切分数量*target正好比num大的话，那么num/切分数量肯定满足比target小

合并相似的物品 - 力扣 (LeetCode) 竞赛

hashmap直接用即可

统计坏数对的数目 - 力扣 (LeetCode) 竞赛

好数概念： i < j 且 j - i == nums[j] - nums[i]， 求好数的个数

明明对做法有印象但就是理不清楚，每次做每次都头晕

主要没法用很简洁的语言表达和解释这个做法

即使我刚做完，我现在也没法很好地描述，为什么是每次put这个nums[i] - i

啊，等等？公式推导？

i < j 且 j - i == nums[j] - nums[i]

那不就是

nums[j] - j == nums[i] - i

即

f[j] == f[i]

f[x] = nums[x] - x

根本和什么动态规划无关，就是一个数学公式推导啊。。。

1
2
3
4
5
6
7
8
9
10

public long countBadPairs(int[] nums) {
    Map<Integer, Long> map = new HashMap<>();
    long result = 0;
    for (int i = 0 ; i < nums.length;i++) {
        int needNum = nums[i] - i;
        result += map.getOrDefault(needNum, 0L);
        map.put(needNum, map.getOrDefault(needNum, 0L) + 1);
    }
    return (long)nums.length * (nums.length-1) /2 - result;
}

任务调度器 II - 力扣 (LeetCode) 竞赛

这个还好，每次完成任务后，存一下下一次任务开始时至少的时间即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution {
    public long taskSchedulerII(int[] tasks, int space) {
        // 存的是下一次任务的至少开始时间
        Map<Integer, Long> map = new HashMap<>();
        long nowTime = 1;
        for (int i = 0; i < tasks.length;i++) {
            int task = tasks[i];
            long canStartTime = map.getOrDefault(task, Long.MIN_VALUE);
            if (nowTime < canStartTime) {
                nowTime = canStartTime;
            }
            map.put(task, nowTime + space + 1);
            nowTime++;
        }
        return nowTime - 1;
    }
}

将数组排序的最少替换次数 - 力扣 (LeetCode) 竞赛

首先我很快想到必须是从右往左去遍历和替换，

如果当前比右边的都要小，则尽可能不拆

如果当前比右边的最小值要大， 则必须拆，拆的时候要保证最小值尽可能大

这题就演变成了

数字x要拆成k个比t小的任意数字，且最小值尽可能小（y)

我固执己见以为是一直按t去减，最后剩余的数字求个平均，就能保证最小值尽可能小了

却没考虑剩余数字可能因为我错误的选择了t导致特别小

实际上应该是拆分后的数字尽可能平均

以100 22为例

5个22正好比100大（4个22比100小）

那么100/5得到的均值肯定比22小

公式上即满足

简单点的话就是 k>=x/y的最小整数，即向上取整

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
    public long minimumReplacement(int[] nums) {
        int n = nums.length;
        long  result = 0;
        int last = nums[n - 1];
        for (int i = n - 2; i >= 0; i--) {
            if (nums[i] > last) {
                
                // k=【num[i] / last】向上取整
                int k = nums[i] / last;
                if (nums[i] % last != 0) {
                    k++;
                }
                last = nums[i] / k;
                result += k-1;
            } else {
                last = nums[i];
            }
        }
        return result;
    }
}

只记录一下对我而言比较有意义的题目

本期总结：#

1. 永远保持冷静，不要激动，下次可以录屏，记录自己的心态和过程
2. 图里有环的判断并不是走回自己，而是走到了重复走过的点

6132. 使数组中所有元素都等于零 - 力扣（LeetCode）

这题花了七分钟，不应该。

题目没看懂

**选出一个正整数 x ，x 需要小于或等于 nums 中 **最小的 非零 元素

又要求最少操作数，那么只能是每次选nums中的最小即可,这里想复杂了，以为是选某个区间范围内的数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

public int minimumOperations(int[] nums) {
    int result = 0;
    for (int i = 0; i < nums.length;i++) {
        int min = getMin(nums);
        if (min == Integer.MAX_VALUE) {
            return result;
        }
        for (int j = 0; j < nums.length;j++) {
            if (nums[j] != 0) {
                nums[j] -= min;
            }
        }
        result++;
    }
    return result;
}

public int getMin(int[] nums) {
    int min = Integer.MAX_VALUE;
    for (int i = 0; i < nums.length;i++) {
        if (nums[i] != 0) {
            min = Math.min(nums[i], min);
        }
    }
    return min;
}

6133. 分组的最大数量 - 力扣（LeetCode）

脑筋急转弯啊这是

跟grades根本没关系

直接排序后，每次取1个、2个、3个即可

拿就是看这样增加到什么时候为止结束

1
2
3
4
5
6
7
8
9
10
11
12

class Solution {
    public int maximumGroups(int[] grades) {
        //Arrays.sort(grades);
        int k = 0;
        int len = grades.length;
        while (len - (k+1) >= 0) {
            len = len - (k+1);
            k++;
        }
        return k;
    }
}

6134. 找到离给定两个节点最近的节点 - 力扣（LeetCode）

这题思路其实也容易想：

先从node1一直往下遍历，直到遇到尽头或者环，记录每个点的距离

1
2
3
4
5
6
7

dis[node1] = 0;
int d = 1;
int node = edges[node1];
while (node != -1 && dis[node] == -1) {
    dis[node] = d++;
    node = edges[node];
}

然后node2也一直往下走，遇到node1走过的点（通过dis是否为-1判断）则计算最小值和要选择的点。同时也要判断环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

d = 0;
node = node2;
int select = 0;
int result = Integer.MAX_VALUE;
boolean[] vis = new boolean[edges.length];
while (node!=-1 && !vis[node]) {
    if (dis[node] != -1) {
        if (Math.max(d, dis[node]) < result) {
            result = Math.max(d, dis[node]);
            select = node;
        }
    }
    d++;
    vis[node] = true;
    node = edges[node];

}

但是自己提前想漏了很多点

遗漏点1：环的判断并不是走回自己啊，而是走到了重复走过的点！

遗漏点2：要注意节点距离相同的情况，要选节点编号最小！

遗漏点3：冷静冷静，不要妄自生气，你及时没进200，也拿到了每日3题的积分了！

这种easy题做了40分钟还错了2次很不应该！

6135. 图中的最长环 - 力扣（LeetCode）

大放水，欸，知道每个点不需要重复走， 这个思路就能处理了

但是要注意 ”碰到自己走过的点即成环了“ 和”碰到别人走过的点，不用再走“是有区别的，不能一起判断

所以我用了一个root来判断

22年8月刷题日记（0730-0817）#

[toc]

2022-07-30#

1175. 质数排列 - 力扣（LeetCode）

简单，题意理解了就好， 排列组合的数学应用

1221. 分割平衡字符串 - 力扣（LeetCode）

简单，推导出贪心规律，从左到右只要符合平衡，就一定可以从更大的平衡串中拆掉

1290. 二进制链表转整数 - 力扣（LeetCode）

“111011011”这种二进制字符串如何快速转int整数？

可以用

1

Integer.parseInt("111011011", 2) 

2指代二进制

2022-07-29#

593. 有效的正方形 - 力扣（LeetCode）

如何用4个点判断是否是一个正方形？

• 方法1： 设置顺时针点为1->2->3->4，然后根据边长相同、22边平行、勾股定理3者判断是否为正方形。

  1->2->3->4点的判定先根据横坐标最小，再根据纵坐标最小。

• 方法二：正方形的任意3个点都是等边直角三角形，判断4次即可，注意额外加一个三角形中边的判断

1
2
3
4

long len = -1;
    public boolean validSquare(int[] a, int[] b, int[] c, int[] d) {
        return calc(a, b, c) && calc(a, b, d) && calc(a, c, d) && calc(b, c, d);
    }

1642. 可以到达的最远建筑 - 力扣（LeetCode）

简单贪心题。

注意PriorityQueue默认小顶堆

1285. 找到连续区间的开始和结束数字 - 力扣（LeetCode）

• row_number() over() 指每一行在整个表分区中的序号

• over()是窗口函数，不会做汇聚动作，因此行数不会发生变化。只会给出每一行所处分区的某个特定值（例如各分区的和 sum over(PARTITION by xxx)）

• id - row_number() over() diff 外层套一个group by diff可以用来求解连续区间的问题

2022-08-01#

剑指 Offer II 082. 含有重复元素集合的组合 - 力扣（LeetCode）

• dfs全排列搜索问题且要求不能重复，关键语句就是”预处理排序。选的时候前一位相同，则必须是连续选的情况，不可以前面的相同数字还没选，却选了自己“

1
2
3

if (i-1 >= 0 && nums[i-1] == nums[i] && lastIndex != i-1) {
      continue;
}

• list.remove(int) 就是按索引移除。 list.remove(object)是针对非int对象的

764. 最大加号标志 - 力扣（LeetCode）

• 写了4个2重循环好麻烦，就是提前预处理好每个点的上下左右到最近0的距离即可

• for (int y = 0, dis=0; y < n;y++) 此时int等同于声明了dis，外层不可再声明dis了

2022-08-03#

2265. 统计值等于子树平均值的节点数 - 力扣（LeetCode）

直接后序遍历即可

541. 反转字符串 II - 力扣（LeetCode）

翻转问题还是写一个reverse的简单方法会比较快，用stringBuilder不一定快

1

void reverse(char[] cs, int left, int right);

575. 分糖果 - 力扣（LeetCode）

集合应用，没啥好说的

2022-08-04#

1403. 非递增顺序的最小子序列 - 力扣（LeetCode）

排序即可

1109. 航班预订统计 - 力扣（LeetCode）

将出点和入点放入数组中，出点位置+seats， 入点位置-seats即可

1115. 交替打印 FooBar - 力扣（LeetCode）

第一次做多线程的题目，还蛮有意思的

要求交替打印n次foo和bat

其实可以用资源的角度来理解

即需要打印foo时，说明生产了一个foo令牌，才可以打印

如果要打印bar，则要求有bar令牌才可以。

那么就很容易想到用2个阻塞队列或者2个信号量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class FooBar {
    private int n;
    private LinkedBlockingDeque<Integer> fooSync = new LinkedBlockingDeque<>();
    private LinkedBlockingDeque<Integer> barSync = new LinkedBlockingDeque<>();

    public FooBar(int n) {
        this.n = n;
        try {
            fooSync.put(1);
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
    }

    public void foo(Runnable printFoo) throws InterruptedException {

        for (int i = 0; i < n; i++) {
            fooSync.take();
            printFoo.run();
            barSync.put(1);
        }
    }

    public void bar(Runnable printBar) throws InterruptedException {

        for (int i = 0; i < n; i++) {
            barSync.take();
            printBar.run();
            fooSync.put(1);
        }
    }
}

当然也可以用一个boolean布尔值来表示此时打印foo还是打印bar，然后利用等待-唤醒机制。

如果用java自带语法，可以是wait和notify。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

class FooBar {
    private int n;
    private int count;        
    public FooBar(int n) {
        this.n = n;
        this.count = 2*n;
    }

    public void foo(Runnable printFoo) throws InterruptedException {

        for (int i = 0; i < n; i++) {
            // printFoo.run() outputs "foo". Do not change or remove this line.
            synchronized (this) {
                if (count%2==1) {
                    this.wait();
                }
                 printFoo.run();
                 count--;
                this.notify();
            }
        }
    }

    public void bar(Runnable printBar) throws InterruptedException {

        for (int i = 0; i < n; i++) {
            // printBar.run() outputs "bar". Do not change or remove this line.
            synchronized (this) {
                if (count%2==0) {
                    this.wait();
                }
                printBar.run();
                count--;
                this.notify();
            }
        }
    }
}

如果使用JUC，则用Condition即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

class FooBar {
        private int n;
        private ReentrantLock lock = new ReentrantLock();
        private Condition condition = lock.newCondition();
        boolean flag;
        public FooBar(int n) {
            this.n = n;
        }

        public void foo(Runnable printFoo) throws InterruptedException {

            for (int i = 0; i < n; i++) {
                lock.lock();
                if (flag == true) {
                    condition.await();
                }
                printFoo.run();
                flag = true;
                condition.signal();
                lock.unlock();
            }
        }

        public void bar(Runnable printBar) throws InterruptedException {

            for (int i = 0; i < n; i++) {
                lock.lock();
                if (flag == false) {
                    condition.await();
                }
                printBar.run();
                flag = false;
                condition.signal();
                lock.unlock();
            }
        }
}

2022-08-05#

1055. 形成字符串的最短路径 - 力扣（LeetCode）

2个字符串长度最多1000，双指针即可，没啥难的

剑指 Offer II 092. 翻转字符 - 力扣（LeetCode）

提前预处理往左看的1的个数和往右看的0的个数

然后再遍历一次，每次把左边翻0，右边翻1，因为预处理过了所以可以马上得到答案

但是这个做法比较消耗2个O(n)的空间

用动态规划可以节省很多空间

1
2
3
4
5
6
7
8
9
10
11
12

public int minFlipsMonoIncr(String s) {
    // dp0代表位置为i时变成000..00所需翻转的数量
    // dp1代表位置为i时变成0001111所需翻转的数量
    int dp0 = 0, dp1 = 0;
    for (int c : s.toCharArray()) {
        int last0 = dp0;
        int last1 = dp1;
        dp0 = last0 + (c=='0' ? 0 : 1);
        dp1 = (c=='1' ? 0 : 1) + Math.min(last0, last1);
    }
    return Math.min(dp0, dp1);
}

409. 最长回文串 - 力扣（LeetCode）

就是数量统计题而已

2022-08-07#

636. 函数的独占时间 - 力扣（LeetCode）

栈的应用题，start和end等同于左括号和右括号

注意用int[]数组来简化新类的定义操作，注意每次end出栈后，要把这段程序占用的总时间加到栈顶

2022-08-08#

1219. 黄金矿工 - 力扣（LeetCode）

提示dfs最大深度为25，则认为可以直接做带vis访问标记的dfs且不需要做记忆化结果。

另外dfs时也不要忘记对初始点的vis处理

1365. 有多少小于当前数字的数字 - 力扣（LeetCode）

虽然是简单题，数量级别只有500，但还是考虑写了一下最快性能，直接按值做键处理，就能知道比每个值小的数量了，然后再分别设置。

761. 特殊的二进制序列 - 力扣（LeetCode）

这题没做出来，直接看答案了

0和1的数量相等 + 任意前缀1数量大于0， 类似于括号匹配

要我们调整括号对使得字典序尽可能大

这样就很容易想到递归了，即最外层括号可以不管， 然后只对内层做处理， 内层找到每一个括号对，然后按字典序排序。

• 字符串list快速拼接：list.stream().collect(Collectors.joining());

• s.subString(a,b)中b是开区间

2022-08-09#

1413. 逐步求和得到正数的最小值 - 力扣（LeetCode）

遍历求和，求中间sum距离1的最大差值即可

1367. 二叉树中的列表 - 力扣（LeetCode）

O(二叉树节点*链表节点)的复杂度符合要求

遍历每个点为起点，然后往下搜索判断能否找到即可，还是挺有意思的递归应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

public boolean isSubPath(ListNode head, TreeNode root) {
    ListNode node = head;
    List<Integer> nodes = new ArrayList<>();
    while(node != null) {
        nodes.add(node.val);
        node = node.next;
    }
    return dfs(root, nodes);
}
boolean dfs(TreeNode node, List<Integer> nodes) {
    if (node == null) {
        return false;
    }
    if(checkToDown(node, nodes, 0)) {
        return true;
    }
    return dfs(node.left, nodes)  ||   dfs(node.right, nodes);
}

boolean checkToDown(TreeNode node, List<Integer> nodes, int index) {
    if (index == nodes.size()) {
        return true;
    }
    if (node == null || node.val != nodes.get(index)) {
        return false;
    }
    
    return checkToDown(node.left, nodes, index+1) || checkToDown(node.right, nodes, index+1);
}

剑指 Offer II 077. 链表排序 - 力扣（LeetCode）

要求在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序

那所有排序方法里，只有递归排序可以实现了

而且得是从下往上递归

先11合并，再22合并，再44合并。

链表归并排序处理的几个坑：

1. 头节点可能变更的话，最好提前创建一个dummy头节点，这样dummy头节点.next就是新节点了
2. 注意记录下一个排序序列的起始节点，用于确认是否第二个序列到末尾结束了。
3. 还要记录上次排序序列的末尾节点， 用于排序后更新 上次末尾节点.next

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

class Solution {
    public ListNode sortList(ListNode head) {
        int len = 1;

        int listLen = 0;
        ListNode node = head;
        while(node != null) {
            listLen++;
            node = node.next;
        }
        
        // 要总是改变头节点的情况下，最好定义一个空头节点用来更新头节点
        ListNode emptyHead = new ListNode();
        emptyHead.next = head;
        while (len < listLen) {
            ListNode preNode = emptyHead;

            ListNode head1 = emptyHead.next;
            while(head1 != null) {
                ListNode head2 = head1;
                // 走过len步，找到第二个比较序列的头部
                for (int i = 0; i < len && head2 != null;i++) {
                    head2 = head2.next;
                }
                // 找不到第二个序列头部了，则不用比较直接结束这次排序
                if (head2 == null) {
                    break;
                }
                
                // 找一下下一次排序序列的开始节点
                ListNode nextSortStartNode = head2;
                for (int i = 0; i < len && nextSortStartNode != null;i++) {
                    nextSortStartNode = nextSortStartNode.next;
                }
                
                // 合并，并更新新合并序列的末尾节点
                ListNode newSortHead = sortBatch(head1, head2, nextSortStartNode);
                // 更新头节点
                preNode.next = newSortHead;
                // 定位末尾节点
                while(preNode.next != nextSortStartNode) {
                    preNode = preNode.next;
                }

                head1 = nextSortStartNode;
            }
            len*=2;
        }
        return emptyHead.next;
    }

    ListNode sortBatch(ListNode head1, ListNode head2, ListNode nextNode) {
        ListNode head3 = new ListNode();
        ListNode node1 = head1;
        ListNode node2 = head2;
        ListNode node3 = head3;
        while(node1 != head2 || node2 != nextNode) {
            int val1 = node1 != head2 ? node1.val : Integer.MAX_VALUE;
            int val2 = node2 != nextNode ? node2.val : Integer.MAX_VALUE;
            if (val1 < val2) {
                node3.next = node1;
                node1 = node1.next;
            } else {
                node3.next = node2;
                node2 = node2.next;
            }
            node3 = node3.next;
        }
        node3.next = nextNode;
        return head3.next;
    }
}

2022-08-10#

1253. 重构 2 行二进制矩阵 - 力扣（LeetCode）

还是蛮容易推导的一个数组题，先处理掉所有0和2的情况

再处理1的情况，先把1都分配给上边，上边不够之后再分配给下边，最后检查是否清零即可。

1102. 得分最高的路径 - 力扣（LeetCode）

很有意思的搜索题，我想到了bfs，且这个bfs是支持刷新点的bfs。先优先按最大的走

如果发现当前点被人走过，但是自己是比他优（不能相等），则可以刷新对方自己继续走。

1
2
3
4
5
6

// 已经有人走过，且自己不能刷新最好记录，则没必要走了，别人已经在走了
if (gMin[ny][nx] != Integer.MIN_VALUE && gMin[ny][nx] >= Math.min(grid[ny][nx], lastMin)) {
    continue;
}
gMin[ny][nx] = Math.min(grid[ny][nx], lastMin);
queue.offer(new int[]{ny, nx, gMin[ny][nx]});

当然看答案还有dfs+二分， 即确定目标最小值之后， dfs搜索最多10000次。

复杂度O(10000 * (log2(10^9)))

剑指 Offer II 024. 反转链表 - 力扣（LeetCode）

用递归做比较有趣

2022-08-11#

1469. 寻找所有的独生节点

直接递归判断，简单

面试题 10.05. 稀疏数组搜索 - 力扣（LeetCode）

二分搜索，但我还是遍历了一遍先过滤空字符串了。导致性能是1ms

但差距不大是因为那些人也要定位后在0上去走，消耗不会差别太大。

1100. 长度为 K 的无重复字符子串 - 力扣（LeetCode）

很简单的滑动窗口

1. 第一波做出来性能20ms，不是最佳。因为用了Stream去判断是否有重复

1
2
3

public boolean valid(int[] counts) {
    return Arrays.stream(counts).noneMatch(c -> c >= 2);
}

2. 去掉Stream改用简单for循环，性能就到 5 ms 了

3. 去掉k>26的判断，提升到4ms

4. 避免每次26次判断，用repeatCount值来记录，这样每次最多判断2次，结果还是4ms

   

1417. 重新格式化字符串

一般那种要你交叉放数字的，都可能有一种改进点是看你能否空间复杂度为O(1)（不包含结果输出空间）

这就需要原地算法，双指针进行交换

2022-08-12#

1282. 用户分组 - 力扣（LeetCode）

按数量建哈希表，每个数量对应一个列表，列表满了就放入结果中并重置，很简单

1423. 可获得的最大点数 - 力扣（LeetCode）

只能取左右两边，那么等同于滑动窗口，只不过是反着求中间的滑动窗口最小值

剑指 Offer II 067. 最大的异或 - 力扣（LeetCode）

很有意思，要求 nums[i] XOR nums[j] 的最大运算 结果

想了半天终于想起来有一个字典树这玩意，一开始觉得麻烦，后来还是写了 ，答案也有这个思路，很棒

只不过自己得记住，要先在字典树中试图求解最大运算结果， 求解完成后，才能把自己再插入字典树中

2022-08-13#

1678. 设计 Goal 解析器 - 力扣（LeetCode）

直接取临时字符串然后判断即可

1874. 两个数组的最小乘积和 - 力扣（LeetCode）

直接排序后第一个数组的最大乘第二个数组的最小，依次处理即可，很简单，虽然我不知道怎么证明 768. 最多能完成排序的块 II - 力扣（LeetCode）

一次就AC了， 想到了动态规划

每次求出左边的最大值

然后看一下自己当前位置往左边遍历时，选取那个左边位置作为一块，能否满足要求，能满足要求则就看判断当前最大分割块即可

1
2
3

if (左边最大值 小于 我当前位置从右往左遍历时的最小值， 说明可以分割){
    dp[当前位置] = Math.max(dp[左边界-1] + 1  , dp[当前位置]);
}

2022-08-15#

641. 设计循环双端队列 - 力扣（LeetCode）

循环双端队列，其实关键在于循环队列的定义，双端的话很容易处理的。

这题肯定是要用数组来做比较有意义

循环队列数组概念硬记忆：

• front指向已存储的队头元素， rear指向已存储的队尾元素的下一个位置（即空位置）

• 队满： (Q.rear+1)%M = Q.front， 即队尾的下一个位置已经有了
• 队空： Q.front = Q.rear 即队头存储的是一个空的
• 队长： (rear-front+M)%M

剑指 Offer 66. 构建乘积数组 - 力扣（LeetCode）

很简单， 直接计算左边前缀乘积， 计算右边前缀乘积即可

1015. 可被 K 整除的最小整数 - 力扣（LeetCode）

• 数字末尾是1的情况下，肯定不能被2和5整除

• 通过公式推导：

  1 2 3 4 5 6 7 8 9

  设n=p*K+q 则n*10+1= 10*p*K + q*10+1; 对两边都取k取余 有(n*10+1)%K=(10*p*K+q*10+1)%K 又因为n%k=q 则右边(10*p*K+q*10+1)%K = (q*10+1)%K = (n%k*10 + 1) %K 推断出：(n*10+1)%K = ((n%K)*10+1)%K 因此(n*10+1)如果能被k整除，等同于 (n%k)*10+1被k整除 所以只要n做增加时先取余即可

不含2和5的质因子的数必定在K之内有解，直接用其mod循环即可，避免了大数之间的除法

2022-08-16#

1656. 设计有序流 - 力扣（LeetCode）

用String[]做数组，当前点之前是空，现在要插入，则可以尝试往后遍历直到遇到空

2278. 字母在字符串中的百分比 - 力扣（LeetCode）

没看懂有啥用

326. 3 的幂 - 力扣（LeetCode）

直接按3取余，不断除3，直到为1说明就是3的幂

题解有个超简单方法：

根据数值范围，找到最大的3幂的值 1162261467 ，然后直接看 1162261467 能否被询问的这个值整除即可

这提示我们如果以后遇到这种需求，可以直接定义一个最大范围值取判断，而不用自己重复去循环计算

1
2
3
4
5

class Solution {
    public boolean isPowerOfThree(int n) {
        return n > 0 && 1162261467 % n == 0;
    }
}

2022-08-17#

914. 卡牌分组 - 力扣（LeetCode）

记住gcd公式：

1
2
3

public int gcd(int x, int y) {
    return x == 0 ? y : gcd(y % x, x);
}

或者这题里因为题目必须要求分成每组X个，所以总数必须要能被X整除，这就过滤掉很多了

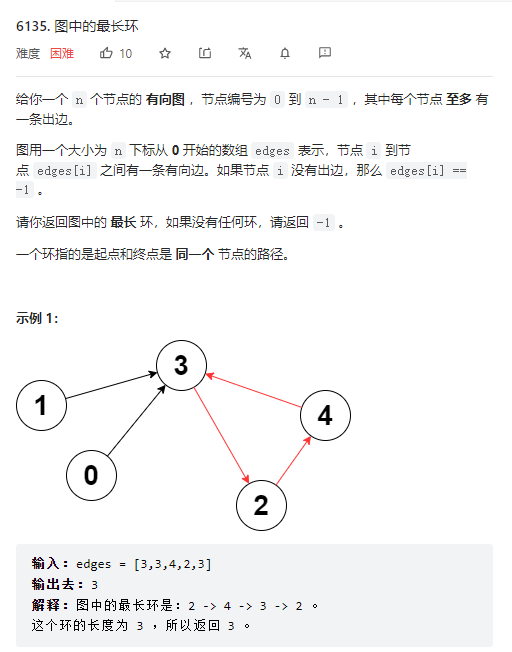
684. 冗余连接 - 力扣（LeetCode）

一个树，加上一个边构成带环的图，问怎么找到应该去掉的那条边，重新变回树

我最初的思路：每次去掉一个边，然后做bfs看是否重新碰到自己的点，但是要考虑很多判断，很麻烦

这题最佳是用并查集， 当拼接的时候，如果发现左右两个点属于同一个集合，则一定会出现环

即是否图中成环的判断可以用这个方式：

通过边连接2个点的时候，如果2个点属于同一个并查集，则一定存在环

1733. 需要教语言的最少人数 - 力扣（LeetCode）

最开始以为我的思路需要500乘500乘500

后来发现其实好友关系的总数只有500，即边只有500个

则遍历次数少了500倍

那可以直接遍历每种语言，判断能否加

注意需要提前处理掉那些不需要新学语言的人（即他和他的所有好友都有共同语言）

[toc]

将下面这些数据库的概念单独拿出来时，相信很多人都有了解或者记忆过，但是将这些概念全部串联在一起时，可能就会很混乱。
我这里举个例子：

• 排他锁、共享锁
• 行锁、表锁、意向锁、间隙锁、next-key锁
• 悲观锁、乐观锁
• 两阶段锁协议
• LCBB锁并发控制协议、MVCC多版本控制协议
• 脏读、不可重复读、幻读
• RU\RC\RR\SE隔离级别
  然后自己问自己一个问题：

1. 这一堆锁的关联关系究竟是什么？
2. 各隔离级别究竟是怎么用各种锁+MVCC来解决事务读问题的？

脏读和脏读过程中涉及的锁#

首先，我们完全不考虑数据库引擎、隔离级别设置之类的，就当作你用一个超简陋的儿科级别数据库来存放和更新数据。

假设你的商城服务正好在同时执行如下的2种事情

• 张三给穷光蛋李四转账100元。
• 李四尝试下单购买100元的衣服

李四在最开始余额只有0元钱。
注意因为是同时执行，在没有做任何保护的情况下，就可能会出现下图这样的情况

可以看到李四明明没有钱，却扣费了，变成了很奇怪的-100元。

Q:同时执行加钱和扣钱操作，一方回滚导致数据出错的读过程叫什么？#

A: 这个过程就叫做脏读。 即更新回退的时，另一个事务读到了脏数据，判断失误，导致做了错误的处理。
根本原因是2个事务都是先查后扣，却没有提前保护的形式

Q: 在不修改数据库隔离级别的情况下， 我们可以如何用sql语句手动解决这个脏读？#

A: 那很显然就是加锁对事务过程做提前保护， 不让B去判断和扣费。
sql语句里有个 ”for update“ 语法， 会手动锁住李四那一行，在调用commit后释放
具体见下面绿色的标注部分：

Q: 刚才看到”锁住李四这一行“， 那么这个就叫行级锁。什么情况下会变成锁住整个表？#

A:
name ='李四’这句话， 如果name是索引列的话，就会加行锁
如果不是索引列， 就会变成表锁。
换言之， 行锁的本质是在索引节点上加锁
如果无法在索引节点上加锁，那就会直接变成整张表的锁，代价就会很大。

另外表锁也可以单独用lock table的语法手动加锁

Q: 如果一个事务A申请了行锁，锁住某一行， 另一个事务B申请了表锁，那B会被阻塞吗？#

A:
B事务既然申请表锁，说明可能会用到A中的每一行。
B申请的流程可以是下面这样：

1. 判断表是否已被其他事务用表锁锁表
2. 判断表中的每一行是否已被行锁锁住。
   但2这一步也太耗时了。
   因此A申请行锁前，会优先申请一个意向锁，再申请行锁。
   然后B申请时，第2步改成判断意向锁即可，有意向锁就阻塞。

简单点说， 意向锁就是行锁操作用来阻塞表锁用的。 但行锁和行锁之间不会互相阻塞，除非行有冲突。

排他锁概念#

刚才看到的for update会限制其他并行事务的所有读写操作，而且是2个事务上都加了”for update“。
那么这个锁就叫做”排他锁“， 属于非常强势的锁， 相当于其他读写操作马上全部拦住了。

这里使用排他锁来解决脏读的原因是因为后面有查询余额+扣余额的代码，写这段代码的人必须做提前保护，以避免自己读到一个可能被修改的数据，导致判断和修改失误。

共享锁概念#

和排他锁对应的是“共享锁”，也就是熟知的读写锁。
可以让多个事务同时读，但是不允许修改 。
手动加共享锁的方式:把for update改成 lock in share mode即可

Q: 那么什么时候使用共享锁比排他锁要好呢？#

A:
可以看下面的例子：

可以看到没有查自身+更新自身的操作， 仅仅是查+更新其他表，表之间也互不关联，对余额的实时性也不是要求太高。

• 如果都加排他锁，各种select操作就会很慢。
• 但如果不加共享锁， T6这边删除时，就可能产生冗余数据，所以还是得加锁。

Q: 那我加的共享锁（S锁）和排他锁（X)什么时候释放呢？是每次执行完update马上释放吗？#

A:
这里就涉及了“两阶段锁”协议。

• 加锁阶段：在该阶段可以进行加锁操作。在对任何数据进行读操作之前要申请并获得S锁（共享锁，其它事务可以继续加共享锁，但不能加排它锁），在进行写操作之前要申请并获得X锁（排它锁，其它事务不能再获得任何锁）。加锁不成功，则事务进入等待状态，直到加锁成功才继续执行。
• 解锁阶段：当事务释放了一个封锁以后，事务进入解锁阶段，在该阶段只能进行解锁操作不能再进行加锁操作。

说人话， 就是在事务中需要加锁时再加锁， 直到commit完一次性解锁。

为什么要两阶段锁，看到的一句话是
若并发执行的所有事务均遵守两段锁协议，则对这些事务的任何并发调度策略都是可串行化的。

Q: 两阶段锁协议可以避免死锁吗？#

A:
不能避免，但是可以通过死锁检测算法进行事务解除。

重新回到张三李四转账+下单的场景上来。
for update这种锁，其实也是一种“悲观锁” ，加锁解锁比较耗时， 默认经常发生竞争。
但如果我的转账和下单过程要求非常快，每次只有几毫秒，那加悲观锁成本就太大了
这时候就可以手动使用乐观锁， 需要你自己在余额表里增加version列，增加后如下所示：

这样就不需要特地加锁了，每次循环判断即可，前提是冲突发生概率比较低，阻塞时间比较短。

刚才一个小小的脏读，就已经解决了下面3个问题

• 排他锁和共享锁的区别：前者是拒绝所有读写 ， 后者是允许并发读拒绝写
• 行锁和表锁的区别： 前者是对单行加锁 ， 后者是对整表加锁， 区别是 是否涉及索引
• 悲观锁和乐观锁的区别： 前者主动用数据库自带的锁， 后者自己添加version版本号
  外加一个两阶段锁协议

隔离级别和MVCC原理#

继续回到脏读问题， 前面我们学习的所有概念，都是和数据库自身隔离级别无关，使用数据库的锁语法或者version版本号来避免。

但数据库发展这么强大，怎么可能需要我们频繁自己写这种复杂逻辑，于是数据库诞生了隔离级别设置。

前面会发生脏读的隔离级别， 叫做RU（read uncommited)
即RU级别时， 我可以在别的事务没完全commit好时就读到数据。

Q: 先来个小问题，RU级别没有任何锁，对吗？#

A:
错误， RU级别做update等增删改操作时，仍然会默认在事务更新操作中增加排他锁，避免update冲突。
切记脏读的发生原因，是查询+更新+回滚时没加锁导致其他查询操作出现失误判断。
即查询这块可能读到没提交的数据，导致错误，而不是更新的并发问题。

Q: 当我们的数据库被设置成RC级别（Read commited）时， 可以解决脏读， 那么背后是怎么解决的呢？#

A:
业界有两种方式

• LBCC基于锁的并发控制（Lock-Based Concurrency Control)）
• MVCC基于多版本的并发控制协议(Multi-Version Concurrency Control)

LBCC其实就是类似前面手动用悲观锁的方式， 事务操作中查询时默认试图加锁，因此就可能被update的排他锁阻塞住，避免了脏读。

但代价就是效率很低。很多场景下，select的次数是远大于update的。

所以InnoDb 基于乐观锁的概念， 想了一个MVCC，自己在事务的背后实现了一套类似乐观锁的机制来处理这种情况。 确保了尽可能不在读操作上加锁， 排他锁只对更新操作生效。

Q: MVCC究竟是怎么做的呢？#

A:
简单来说，就是默认给每个数据行加了一个版本号列TRX_ID和回滚版本链ROLL_BT，具体可以看《高性能mysql》书里的这段描述：

简而言之

• 查的时候，只查当前事务之前的记录，或者回滚版本比当前大的已删记录。
• 增的时候，加新版本的记录
• 删的时候，把老记录标记上回滚版本
• 改的时候，本质上是加新记录， 同时把老记录标上回滚版本

Q: MVCC机制下， 什么是快照读，什么是当前读？#

A:

• 快照读：对于select读操作，统一默认不加锁，使用历史版本数据。
• 当前读：对于insert、update、delete操作，仍然需要加X锁，因为涉及了数据变更，必须使用最新数据进行修改

Q: 那么回到刚才的脏读问题， MVCC究竟是怎么在读不加锁的情况下， 解决脏读的？#

A:
首先，每次select都不用任何锁， 每次都是快照读，不会阻塞，因此会变成下面这样：

总结这个图，就是

1. 每次读时，会生成一个readView，用来记录当前还没提交的事务版本号。
2. 根据自己事务的版本号version，去寻找小于自己当前版本且不在readView集合中的记录。

这样的话就保证了读的数据必须是已经完成提交的，是不是很简单？

Q: 如果事务B中不做余额判断，支持直接赊账+扣费， 那是不是会导致先扣费，然后回滚成0这样的情况？#

A:
不会。
上面提过， MVCC中更新操作都是“当前读”，仍然需要加X锁， 且因为涉及了数据变更，必须使用最新数据版本进行修改

换言之， update等操作， 还是会加锁，且用最新版本更新，避免了脏更新的问题，如下：

Q: 上面这个过程有什么隐患#

A:
如果1个事务中连续读2次余额，可能有“不可重复读”的风险，即前后读的数据发生了不一致
如下所示

因此RC隔离级别无法解决 “不可重复读的问题”

Q: RR（可重复读，Repeat Read)的隔离级别又是怎么解决上面这个问题的？#

A:
本质上就是readView生成时的区别
上面RC不可重复读的图中可以看到，每次读时，都取了最新的readView。 这可能导致事务A提交后， 事务B观察到的readView集合发生了变化。

因此RR机制改变了readView的生成方式， 每次读时只使用事务B最开始拿到的那个readView，这样永远就只取老的数据了。

Q: 那读问题中的幻读又是什么？#

A:
刚才的”不可重复读“，是一个事务中查询2次结果，发现值对不上。
而”幻读“，是指一个事务中查询2批结果，发现这2批数量对不上，就好象发生了幻觉。
就像下图所示展示：

Q: RR隔离级别中的MVCC机制可以解决上面的问题吗？#

A:
可以解决。
通过查询的快照读，能够保证只查询到同一批数据。

Q: 那如果像下面这样， 事务A连续做两次更新呢，单纯靠MVCC能避免更新操作的幻读么？#

A:
如果只依靠MVCC，那就无法避免了， 因为update操作是”当前读“，每次取最新版本做更新， 这会导致update中的读操作出现幻读，前后更新的记录数量不一样了。

Q: 那数据库怎么处理这种2次updete中间做insert的幻读情况呢？#

A:
之前有了解到， update过程仍然会加锁，

RR级别会启用一个叫”间隙锁“（Gap锁）的玩意，专门来防这样情况。
即调用 update xxx where name ='李四’时， 不仅仅在李四的行上加锁， 更会在中间所有行的间隙、左右边界的两边，加上一个gap间隙锁，就像下面这个图一样：

可以看到，订单D的插入过程被update过程的间隙锁拦住了，于是无法插入，置到事务结束才会释放。
因此事务中两次update之间的幻读是可以避免的，也能。

Q: 那行锁、间隙锁、next-key锁是什么区别？#

A:
行锁就是单个行（单个索引节点）加锁
间隙锁就是在行（索引节点之间）加锁
next-key就是“行锁+间隙锁”，一起使用。

Q: 如果name这个字段不是索引，而是普通字段，那间隙锁会怎么加？#

A:
那就会给整个表的所有间隙都加上锁！
因为数据库无法确认到底是哪个范围，所以干脆全加上。
这就会导致整表锁住，性能很差。

Q: 那是不是只要name是索引，就不会给整个表全加间隙锁了？#

A:
不对， 如果where条件写的有问题，不符合最左匹配原则，那也会导致索引失效， 以至于给整个表加锁。

Q: 刚才看到说RR可以解决2次select之间的幻读， 也能解决2次update之间的幻读， 那为什么很多资料里，仍然说RR不能解决幻读？#

A:
这个问题我也是翻了好多资料， 终于找到了一个合理的解释。
看下面这个场景：

发现什么区别没， 事务B的insert操作，发生在了事务A的update之前。因此事务B的insert操作没有被间隙锁阻塞。

而update用的是当前读， 于是更新的数量和 最初select的数量匹配不上了。

Mysql官方给出的幻读解释是：只要在一个事务中，第二次select多出了row就算幻读，所以这个场景下，算出现幻读了。

这也就是下面这个图的来源：

Q: 那串行化serializable隔离级别，为什么就能避免幻读了？#

A:
Se级别时，会从MVCC并发控制退化为基于锁的并发控制（LCBB）。
不区别快照读和当前读
所有的读操作都是当前读，读加读锁(S锁)，写加写锁(X锁)。在该隔离级别下，读写冲突，因此并发性能急剧下降，在MySQL/InnoDB中不建议使用。

这就是我们文章最开头手动加锁的那个过程了。