组合数（排列组合）

• C（k,n)的O(Min(k,n-k)）解法：
• 杨辉三角打表法：
  • 如果用O(N)的复杂度，O（1）的空间求解C(n,m)?
• 超大组合数（涉及取余）
• 相关题目

[toc]

C（k,n)的O(Min(k,n-k)）解法：#

快速回想组合数解法：
C(8,3) = 8 * 7 * 6 /(321) = 6 / 1 * 7 / 2 * 8 / 3
即分子和分母的个数是一样的
然后你要从小的开始逐步做乘和除的操作，就能求出来了，且一定能保证整除

public int c(int k, int n) {
    long result = 1;
    // y/x * (y+1)/(x+1)
    for (int y = k+1, x= 1;y<=n && x<=k;y++,x++) {
        // (result*y)一定能被x整除
        result = (result * y) / x;
    }

    return (int)result;
}

杨辉三角打表法：#

如果空间没要求， 但是要求每次快速获取，则可以用杨辉三角提前打表

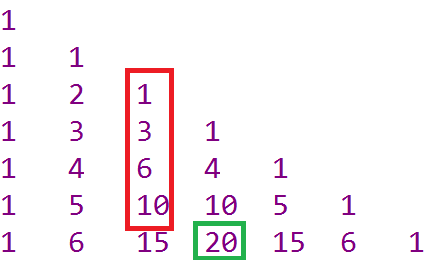
for(int i=0;i<=n;i++){
	c[i][0]=c[i][i]=1;
	for(int j=1;j<i;j++)
		c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}

``

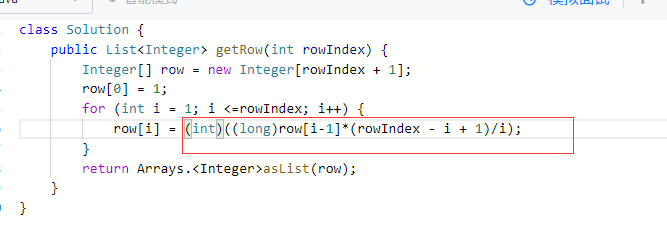
如果用O(N)的复杂度，O（1）的空间求解C(n,m)?#

杨辉三角里，某行某列的值等同于C(n,m)

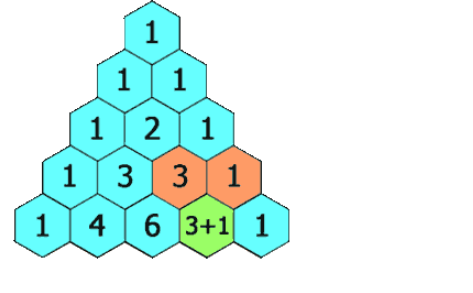
因此可以很短的复杂度得到值
也可以缓存

超大组合数（涉及取余）#

超纲题

• 乘法逆元+快速幂+阶乘
• Lucas定理

总结组合数的几种求法（模板）

---

相关题目#

62. 不同路径 需要空间为1时，必须用组合数
119. 杨辉三角 II O(1)空间求某行某列，用组合数性质