[toc]
第一题:全排列问题,字符串处理麻烦
1087. 花括号展开 - 力扣(LeetCode)
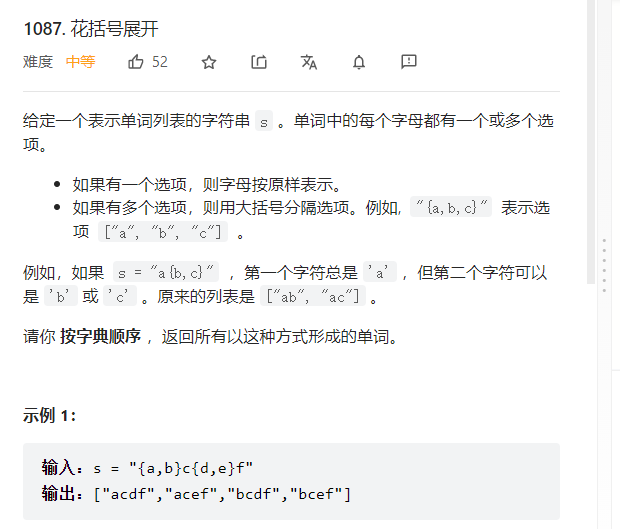
很常见的搜索全排列题
但是处理这个字符串折腾了我好久,看我下面这个也太麻烦了
1
2
3
4
5
6
7
| List<char[]> lists = new ArrayList<>();
String[] split = ss.split(",");
char[] cs = new char[split.length];
for (int j = 0; j < split.length;j++){
cs[j] = split[j].charAt(0);
}
lists.add(cs);
|
看看答案怎么做的,好像其他人都是逐个判断的。

也是,频繁substring还是很耗时间的,不建议
我的答案:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| class Solution {
public String[] expand(String s) {
List<char[]> lists = new ArrayList<>();
for (int i = 0; i < s.length();i++) {
if (s.charAt(i) != '{') {
lists.add(new char[]{s.charAt(i)});
} else {
int end = s.indexOf("}", i);
String ss = s.substring(i+1, end);
String[] split = ss.split(",");
char[] cs = new char[split.length];
for (int j = 0; j < split.length;j++){
cs[j] = split[j].charAt(0);
}
lists.add(cs);
i = end;
}
}
List<String> res = new ArrayList<>();
dfs(lists, 0, new StringBuilder(), res);
Collections.sort(res);
return res.toArray(new String[0]);
}
void dfs(List<char[]> lists, int index, StringBuilder sb, List<String> res) {
if (index == lists.size()) {
res.add(sb.toString());
return;
}
for (char c : lists.get(index)) {
sb.append(c);
dfs(lists, index+1, sb, res);
sb.deleteCharAt(sb.length()-1);
}
}
}
|
第二题:简单动态规划
2244. 完成所有任务需要的最少轮数 - 力扣(LeetCode)
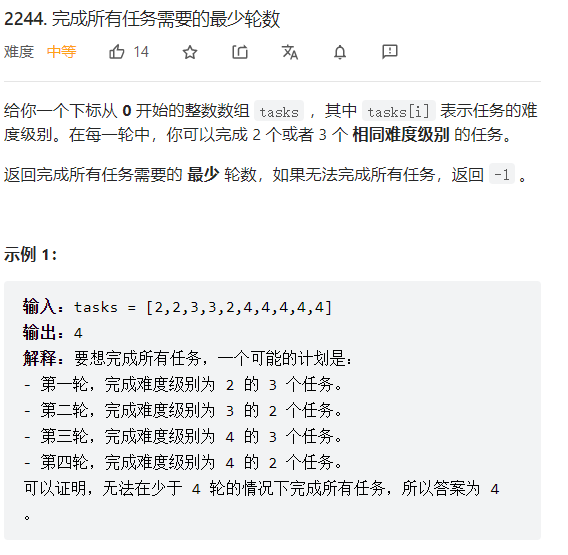
一眼想到动态规划,但就是要注意题意得先排序,还要注意溢出的问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public int minimumRounds(int[] tasks) {
long[] dp = new long[tasks.length];
Arrays.sort(tasks);
for (int i = 0; i < dp.length;i++) {
int task = tasks[i];
dp[i] = Integer.MAX_VALUE;
for (int j = i-1;j>=i-2 && j >=0;j--) {
if (tasks[j] != task) {
break;
}
dp[i] = Math.min(dp[i], 1 + (j-1>=0?dp[j-1]:0));
}
}
return dp[tasks.length-1] >=Integer.MAX_VALUE ? -1 : (int)dp[tasks.length-1];
}
}
|
第三题:通过数据范围决定用动态规划而不是搜索
剑指 Offer II 104. 排列的数目 - 力扣(LeetCode)

看起来以为要搜索,结果一看数据范围:

target最大1000,且都是正数,那么可以直接基于总和做动态规划了,因为不会有超过target的情况出现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target+1];
dp[0] = 1;
for (int sum = 1; sum <= target;sum++ ) {
for (int num : nums) {
if (sum - num < 0) {
continue;
}
dp[sum] += dp[sum - num];
}
}
return dp[target];
}
}
|




