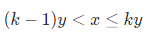
只记录一下对我而言比较有意义的题目
本期总结:
-
遇到类似坐标 j - i == nums[j] - nums[i]的题目,记得直接转移公式以期望得到一个f(x)从而建立基于f(x)做key的hashmap, 不要想着什么从左往右+多少减多少这种绕来绕去的思路。
-
数字num要拆成任意个比Target小的任意数字,且还要拆后的最小值尽可能大,那肯定不是直接基于target去做减法,而是让数字尽可能平均, 切分数量*target正好比num大的话,那么num/切分数量肯定满足比target小
合并相似的物品 - 力扣 (LeetCode) 竞赛
hashmap直接用即可
统计坏数对的数目 - 力扣 (LeetCode) 竞赛
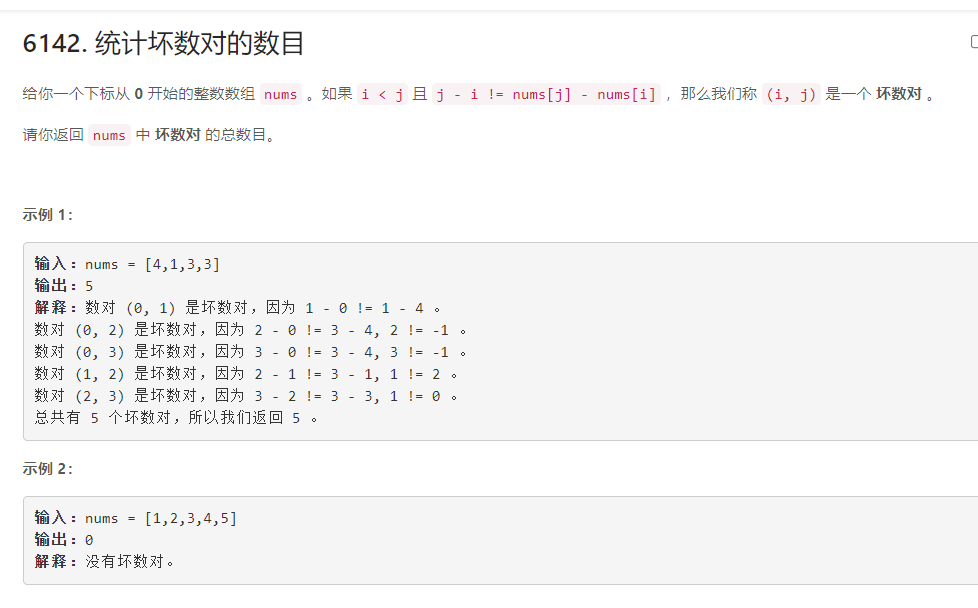
好数概念: i < j 且 j - i == nums[j] - nums[i], 求好数的个数
明明对做法有印象但就是理不清楚,每次做每次都头晕
主要没法用很简洁的语言表达和解释这个做法
即使我刚做完,我现在也没法很好地描述,为什么是每次put这个nums[i] - i
啊,等等?公式推导?
i < j 且 j - i == nums[j] - nums[i]
那不就是
nums[j] - j == nums[i] - i
即
f[j] == f[i]
f[x] = nums[x] - x
根本和什么动态规划无关,就是一个数学公式推导啊。。。
1
2
3
4
5
6
7
8
9
10
| public long countBadPairs(int[] nums) {
Map<Integer, Long> map = new HashMap<>();
long result = 0;
for (int i = 0 ; i < nums.length;i++) {
int needNum = nums[i] - i;
result += map.getOrDefault(needNum, 0L);
map.put(needNum, map.getOrDefault(needNum, 0L) + 1);
}
return (long)nums.length * (nums.length-1) /2 - result;
}
|
任务调度器 II - 力扣 (LeetCode) 竞赛
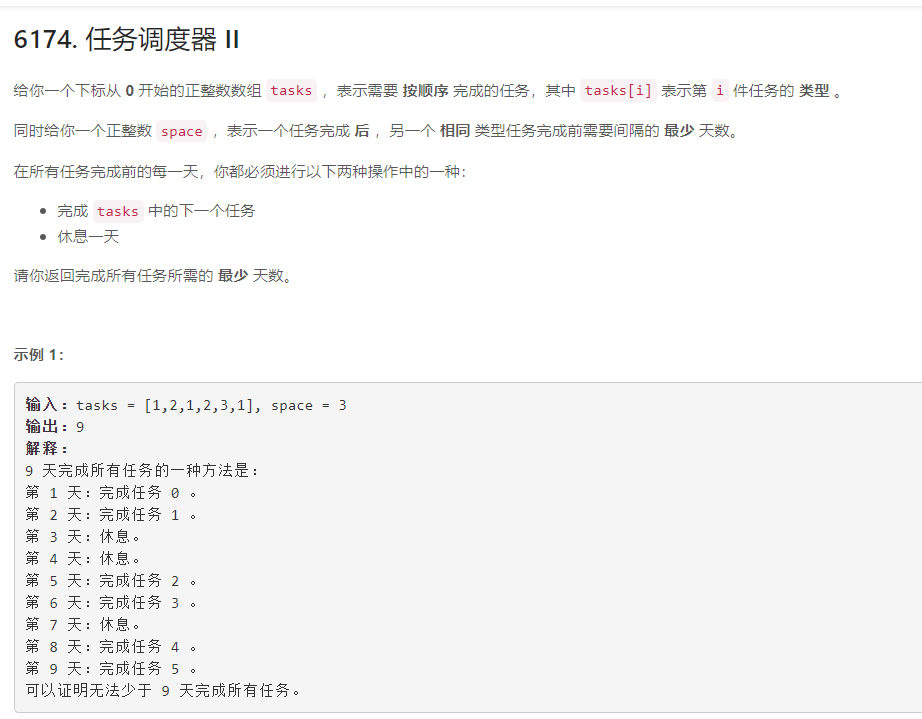
这个还好,每次完成任务后,存一下下一次任务开始时至少的时间即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public long taskSchedulerII(int[] tasks, int space) {
Map<Integer, Long> map = new HashMap<>();
long nowTime = 1;
for (int i = 0; i < tasks.length;i++) {
int task = tasks[i];
long canStartTime = map.getOrDefault(task, Long.MIN_VALUE);
if (nowTime < canStartTime) {
nowTime = canStartTime;
}
map.put(task, nowTime + space + 1);
nowTime++;
}
return nowTime - 1;
}
}
|
将数组排序的最少替换次数 - 力扣 (LeetCode) 竞赛
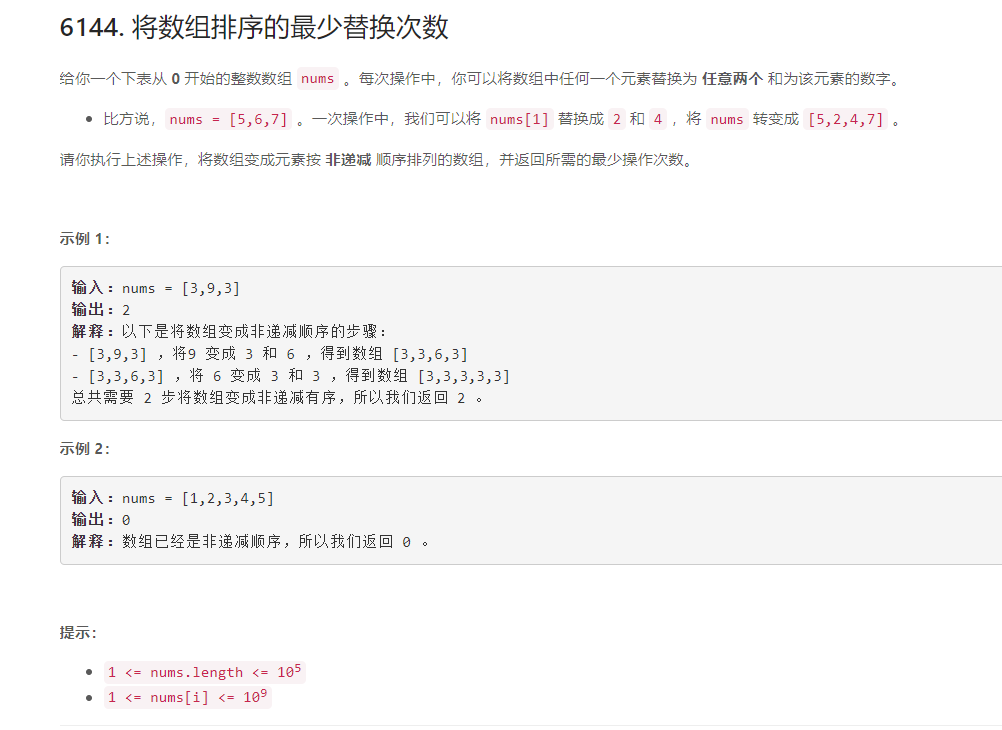
首先我很快想到必须是从右往左去遍历和替换,
如果当前比右边的都要小,则尽可能不拆
如果当前比右边的最小值要大, 则必须拆,拆的时候要保证最小值尽可能大
这题就演变成了
数字x要拆成k个比t小的任意数字,且最小值尽可能小(y)
我固执己见以为是一直按t去减,最后剩余的数字求个平均,就能保证最小值尽可能小了
却没考虑剩余数字可能因为我错误的选择了t导致特别小
实际上应该是拆分后的数字尽可能平均
以100 22为例
5个22正好比100大(4个22比100小)
那么100/5得到的均值肯定比22小
公式上即满足
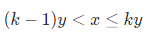
简单点的话就是 k>=x/y的最小整数,即向上取整
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public long minimumReplacement(int[] nums) {
int n = nums.length;
long result = 0;
int last = nums[n - 1];
for (int i = n - 2; i >= 0; i--) {
if (nums[i] > last) {
int k = nums[i] / last;
if (nums[i] % last != 0) {
k++;
}
last = nums[i] / k;
result += k-1;
} else {
last = nums[i];
}
}
return result;
}
}
|