
本期总结:
- 子数字、子序列的题目, 一定要关注一下有没有”连续“二字!
- 排列组合公式可以记忆一下,特别是C二维数组中左边是啥,右边是啥
2399. 检查相同字母间的距离 - 力扣(LeetCode)
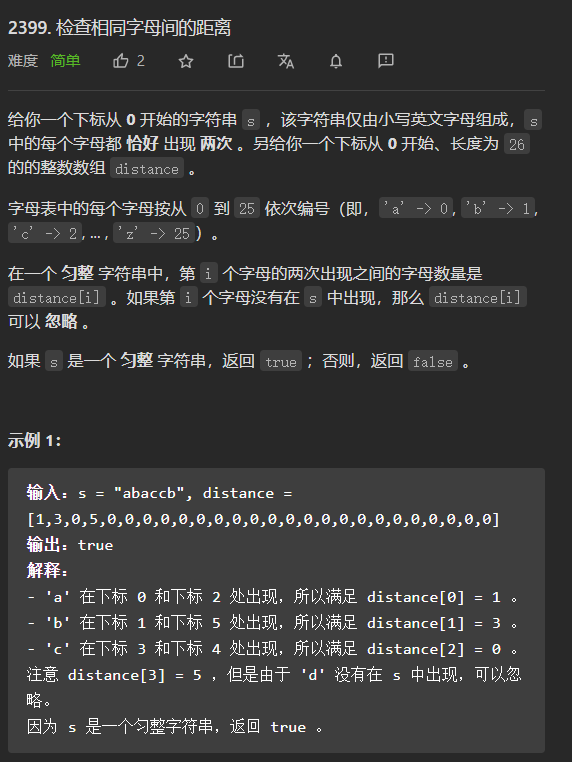
直接2个遍历找距离即可,因为每个字母恰好是2次!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public boolean checkDistances(String s, int[] distance) {
for (int i = 0; i < s.length();i++) {
char c = s.charAt(i);
for (int j = i+1;j<s.length();j++) {
if (c == s.charAt(j)) {
int len = j - i - 1;
if (distance[c-'a'] != len) {
return false;
}
}
}
}
return true;
}
}
|
2400. 恰好移动 k 步到达某一位置的方法数目 - 力扣(LeetCode)
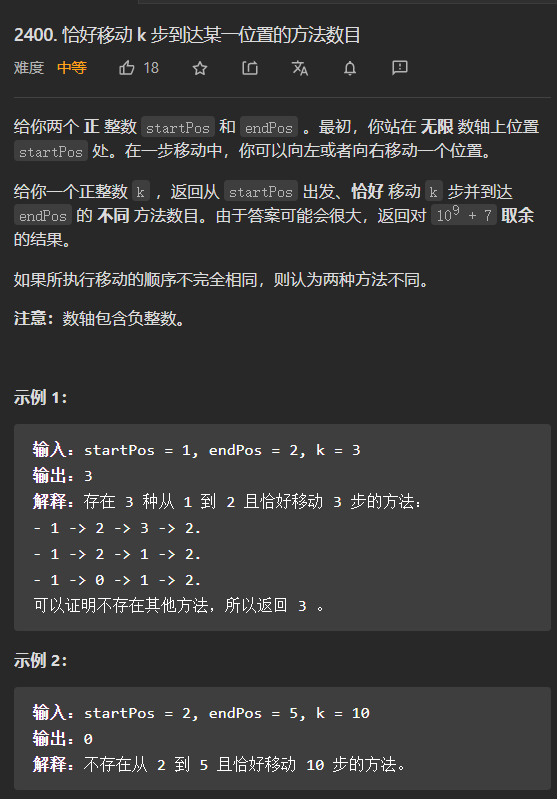
这个题目为啥想了20分钟。。
很明显左移和右移的个数是确定的!
那基本就是排列组合了,结果那个排列组合的方法又整了半天,组合数的计算方式总是记不住!
个数少的时候,直接杨辉三角解法即可, 注意我这个是c[n][m], n是大的那个!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public class Solution {
public int numberOfWays(int startPos, int endPos, int k) {
int cha = Math.abs(startPos - endPos);
int chak = k - cha;
if (chak %2 == 1) {
return 0;
}
if (chak < 0) {
return 0;
}
int k1 = cha + chak/2;
int k2 = chak/2;
int mod = 1000000007;
long[][] c = new long[k+1][k+1];
for(int i=0;i<=k;i++){
c[i][0]=c[i][i]=1;
for(int j=1;j<i;j++)
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
return (int)c[k][k1];
}
}
|
2401. 最长优雅子数组 - 力扣(LeetCode)
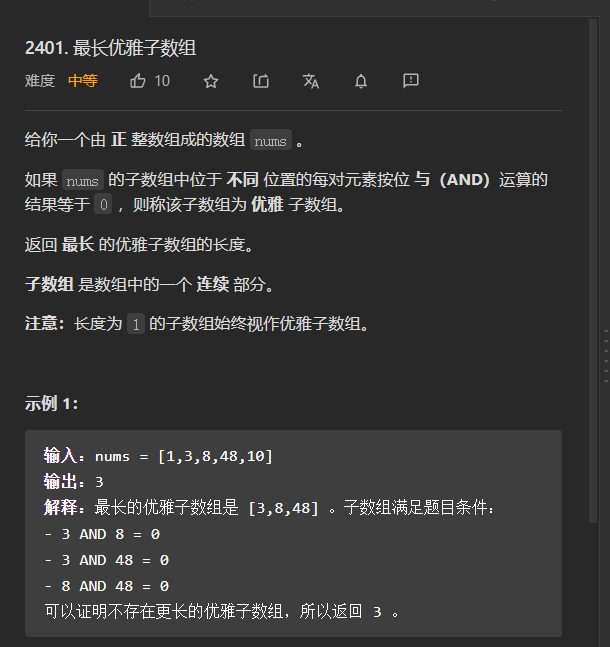
我TM又没看到“连续”二字!!!题目里也没有体现!
以后看到子数组和子序列都注意啊!注意是不是连续,我十多分钟都花在怎么处理非连续了!
知道连续以后就很容易了,记录最左边那个会造成同位1,然后时刻更新最左边的有效点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public int longestNiceSubarray(int[] nums) {
int[] indexNears = new int[33];
Arrays.fill(indexNears, -1);
int lastLeft = 0;
int res = 0;
for (int i = 0; i < nums.length;i++) {
int num = nums[i];
int k = 0;
int novalidLeft = -1;
while (num > 0) {
if (num % 2 == 1) {
novalidLeft = Math.max(novalidLeft, indexNears[k]);
indexNears[k] = i;
}
num/=2;
k++;
}
int canValidLeft = novalidLeft + 1;
if (canValidLeft > lastLeft) {
lastLeft = canValidLeft;
}
res = Math.max(res, i - lastLeft + 1);
}
return res;
}
}
|
2402. 会议室 III - 力扣(LeetCode)
等待后面纳入日常中重新写
题目我会做,就是几个细节没处理好导致gg,主要就是优先队列的比较函数
- 当同时有几个会议室需要释放时, 需要选最小的会议室先出队,这导致我的优先队列比较函数非常关键
- 会议延期要放入一个常规队列,且需要更新时间,还要对原先优先队列里的结束时间做过期处理
- 注意int范围越界,特别是比较函数不可以直接a[0] - b[0],都可能越界
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| class Solution {
public int mostBooked(int n, int[][] meetings) {
long[][] newMeetins = new long[meetings.length][2];
for (int i = 0; i < meetings.length;i++) {
newMeetins[i] = new long[]{meetings[i][0], meetings[i][1]};
}
int j = 0;
int[] places = new int[newMeetins.length];
Queue<long[]> meets = new PriorityQueue<>((a,b)->(!(a[1] == b[1] && a[0] == 1 && b[0] == 1) ? ( a[1] >= b[1] ? 1 : -1) :(places[(int)a[2]] - places[(int)b[2]])));
for (long[] meet : newMeetins) {
meets.add(new long[]{0, meet[0], j});
meets.add(new long[]{1, meet[1], j});
j++;
}
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
priorityQueue.addAll(IntStream.range(0, n).boxed().collect(Collectors.toSet()));
Queue<Integer> waitList = new LinkedList<>();
Set<Integer> waitSet = new HashSet<>();
int[] meetHappendCounts = new int[n];
while (!meets.isEmpty()) {
long[] meet = meets.poll();
long time = meet[1];
int meetIndex = (int)meet[2];
if (meet[0] == 0) {
if (!priorityQueue.isEmpty()) {
int place = priorityQueue.poll();
meetHappendCounts[place]++;
places[meetIndex] = place;
} else {
waitList.offer(meetIndex);
waitSet.add(meetIndex);
}
} else {
if (newMeetins[meetIndex][1] != time) {
continue;
}
if (waitSet.contains(meetIndex)) {
continue;
}
int place = places[meetIndex];
if (!waitList.isEmpty()) {
int waitmeet = waitList.poll();
waitSet.remove(waitmeet);
long startTime = newMeetins[waitmeet][0];
long endTime = newMeetins[waitmeet][1];
long use = endTime - startTime;
long newEndTime = time + use;
newMeetins[waitmeet][1] = (long)newEndTime;
meets.offer(new long[]{1, newEndTime, waitmeet});
places[waitmeet] = place;
meetHappendCounts[place]++;
} else {
priorityQueue.offer(place);
}
}
}
int max = 0;
int select = 0;
for (int i = 0; i < n;i++) {
if (meetHappendCounts[i] > max) {
max = meetHappendCounts[i];
select = i;
}
}
return select;
}
}
|



