第303场周赛-463名-4题（pair类、var特性、双指针而不是二分）

• 本期总结：
• 2352. 相等行列对
• 2353. 设计食物评分系统 - 力扣（LeetCode）
• 2354. 优质数对的数目 - 力扣（LeetCode）

只记录一下对我而言比较有意义的题目

本期总结：#

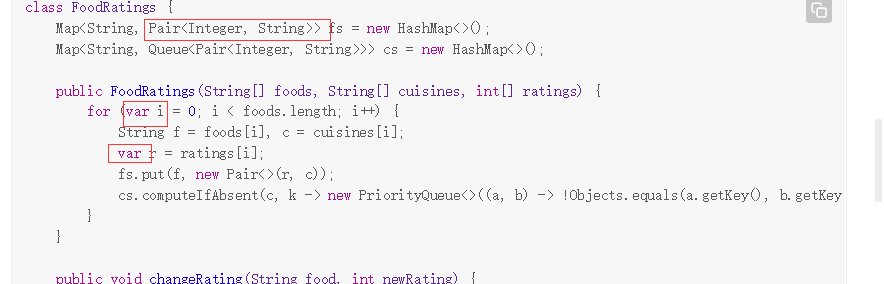
1. 考虑用Pair包装而不是设计class实体类
2. var特性可以简化变量名的打印
3. 双点有序(>k)等问题，优先考虑用双指针而不是二分， 先确定固定哪个点，再看怎么移动，最多就4种情况。

#

看着很简单啊，我的想法是直接对每一行搞成一个字符串， 然后做成hasMap，记录这个字符串出现的次数

在拿列去map里匹配即可

结果忘记了数字的范围是1-10^9， 并非0-9，不能直接拼，还得加逗号。痛失五分钟。

class Solution {
    public int equalPairs(int[][] grid) {
        int ylen = grid.length;
        int xlen = grid[0].length;
        String[] rows = new String[ylen];
        String[] cols = new String[xlen];
        Map<String, List<Integer>> map = new HashMap<>(); 
        for (int y = 0; y < ylen;y++) {
            StringBuilder sb = new StringBuilder();
            for (int x = 0; x < xlen;x++) {
                sb.append(grid[y][x]).append(",");
            }
            String s = sb.toString();
            if (!map.containsKey(s)) {
                map.put(s, new ArrayList<>());
            }
            map.get(s).add(y);
        }
        
        int count = 0;
        for (int x = 0; x < xlen;x++) {
            StringBuilder sb = new StringBuilder();
            for (int y = 0; y < ylen;y++) {
                sb.append(grid[y][x]).append(",");
            }
            String s = sb.toString();
            if (map.containsKey(s)) {
                count += map.get(s).size();
            }
        }
        return count;
    }
}

另外java处理字符串和map问题确实比python要麻烦，如果要冲速度，我是不是得学一下python？

题解里的python，可以快速转数量统计的map

class Solution:
    def equalPairs(self, grid: List[List[int]]) -> int:
        cnt = Counter(tuple(row) for row in grid)
        return sum(cnt[col] for col in zip(*grid))

#

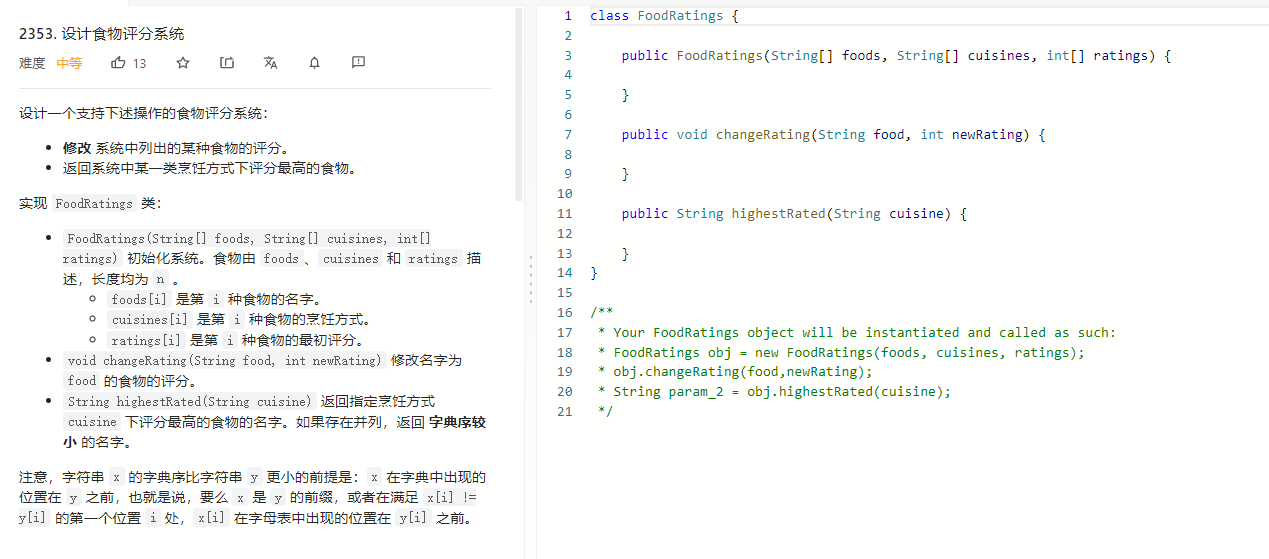
很明显就是一个会更新的优先队列集合

需要用优先队列加一个检查更新的map实现。

    class FoodRatings {

         class Food {
            String name;
            String cuisines;
            int rate;

            public Food(String name, String cuisines, int rate) {
                this.name = name;
                this.cuisines = cuisines;
                this.rate = rate;
            }
        }
        
        Map<String, Queue<Food>> queues;
        Map<String, Food> nowFoodMap = new HashMap<>();
        public FoodRatings(String[] foods, String[] cuisines, int[] ratings) {
            int len = foods.length;
            queues = new HashMap<>();
            for (int i = 0;i<len;i++) {
                Food food = new Food(foods[i], cuisines[i], ratings[i]);
                nowFoodMap.put(foods[i], food);

                if (!queues.containsKey(cuisines[i])) {
                    queues.put(cuisines[i], new PriorityQueue<>((a,b)->(
                            a.rate != b.rate ? (b.rate - a.rate): (a.name.compareTo(b.name)))));
                }
                queues.get(cuisines[i]).offer(food);
            }
        }

        public void changeRating(String food, int newRating) {
            String cu = nowFoodMap.get(food).cuisines;
            Food food1 = new Food(food, cu, newRating);
            nowFoodMap.put(food, food1);
            queues.get(cu).offer(food1);
        }

        public String highestRated(String cuisine) {
            Queue<Food> queue = queues.get(cuisine);
            while (!queue.isEmpty()) {
                Food food = queue.peek();
                if (food != nowFoodMap.get(food.name)) {
                    queue.poll();
                } else {
                    return food.name;
                }
            }
            return null;
        }
    }


/**
 * Your FoodRatings object will be instantiated and called as such:
 * FoodRatings obj = new FoodRatings(foods, cuisines, ratings);
 * obj.changeRating(food,newRating);
 * String param_2 = obj.highestRated(cuisine);
 */

但是定义类的时候比较麻烦，后面可以考虑以下的效率优化：

1. 用Pair做二元组，避免定义内部类麻烦

2. 用var避免定义变量类型

#

其实这个脑筋急转弯通过纸上推演，很快能得到

num1 OR num2 和 num1 AND num2 的1的个数，等同于num1和num2中1的个数总和

就变成就一个数组中，a[x] + a[y]共有多少对

这个子问题的解法我想复杂了，竟然想到用二分法。。。又因为很久没写了，对二分不熟了，导致浪费了大量时间确认二分如下：

class Solution {
    public long countExcellentPairs(int[] nums, int k) {
        Set<Integer> set = Arrays.stream(nums).mapToObj(Integer::valueOf).collect(Collectors.toSet());

        int[] ontCounts = new int[set.size()];
        int[] newNums = new int[set.size()];
        int t = 0;
        for (int s : set) {
            newNums[t++] = s;
        }
        nums = newNums;

        for (int i = 0; i < nums.length;i++) {
            ontCounts[i] = Integer.bitCount(nums[i]);
        }
        Arrays.sort(ontCounts);

        long result = 0;
        for (int i = 0; i < nums.length;i++) {
            int oneCount = ontCounts[i];
            int needOneCount = k - oneCount;

            int left = 0, right = nums.length;
            while (left < right) {
                int mid =  left + (right - left)/2;
                if (ontCounts[mid] < needOneCount) {
                    left = mid+1;
                } else if (ontCounts[mid] >= needOneCount){
                    right = mid;
                } else {
                    break;
                }
            }
            int select = right;
            result += Math.max(0, ontCounts.length - select);
        }
        return result;
    }
}

比二分要更快速的可能是用双指针求解这类问题

但是双指针的方向可能要好好想想

即2个指针哪个优先固定， 再移动哪个，哪个方向移动

这题需要left=0, right=length， 固定住left， 让right移动找到一个位置后，right右边的所有点和left想家肯定都满足> k

long result = 0;
int left = 0, right = ontCounts.length - 1;
for (;left<ontCounts.length;left++) {
    while (right >=0 && ontCounts[left] + ontCounts[right] >= k) {
        right--;
    }
    result += (ontCounts.length - 1 - right);
}